
分析 根据平面向量共线定理的坐标表示,利用正弦定理求出A的值,
再利用同角的三角函数关系和三角恒等变换化简三角函数式μ,即可求出它的取值范围.
解答 解:∵向量$\overrightarrow q$=(2a,1),$\overrightarrow p$=(2b-c,cosC),且$\overrightarrow p$∥$\overrightarrow q$,
∴2acosC-1×(2b-c)=0,
根据正弦定理,得2sinAcosC-(2sinB-sinC)=0,
又∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴2cosAsinC-sinC=0,即sinC(2cosA-1)=0;
∵C是三角形内角,sinC≠0,
∴2cosA-1=0,可得cosA=$\frac{1}{2}$;
∵A是三角形内角,
∴A=$\frac{π}{3}$;
∴三角函数式μ=$\frac{-2cos2C}{1+tanC}$+1
=$\frac{2{(sin}^{2}C{-cos}^{2}C)}{1+\frac{sinC}{cosC}}$+1
=2cosC(sinC-cosC)+1
=sin2C-cos2C,
=$\sqrt{2}$sin(2C-$\frac{π}{4}$),
∵A=$\frac{π}{3}$,得C∈(0,$\frac{2π}{3}$),
∴2C-$\frac{π}{4}$∈(-$\frac{π}{4}$,$\frac{13π}{12}$),可得-$\frac{\sqrt{2}}{2}$<sin(2C-$\frac{π}{4}$)≤1,
∴-1<$\sqrt{2}$sin(2C-$\frac{π}{4}$)≤$\sqrt{2}$,
即三角函数式μ=$\frac{-2cos2C}{1+tanC}$+1的取值范围是(-1,$\sqrt{2}$].
故答案为:(-1,$\sqrt{2}$].
点评 本题考查了平面向量共线定理的坐标表示以及正弦定理,同角的三角函数关系和三角恒等变换的应用问题,是综合性题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
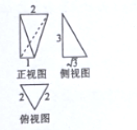
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
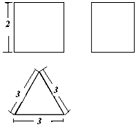 一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是( )
一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在同一个球面上,则这个球的表面积是( )| A. | 16π | B. | 12π | C. | 8π | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{e}$ | B. | $\frac{2}{e}$ | C. | e | D. | 2e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
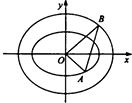 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com