
分析 当命题p为真时,△<0.当命题q为真时,4-3a>1.由p或q为真,p且q为假,p,q为一真一假,即可得出.
解答 解:当命题p为真时,△=4a2-16<0,(1分) 所以-2<a<2.(2分)
当命题q为真时,4-3a>1,(3分)所以a<1. (4分)
因为p或q为真,p且q为假,p,q为一真一假.(5分)
当p真q假时,$\left\{\begin{array}{l}{-2<a<2}\\{a≥1}\end{array}\right.$,(6分)
所以1≤a<2. (7分)
当p假q真时,$\left\{\begin{array}{l}{a≤-2或a≥2}\\{a<1}\end{array}\right.$,(8分)
所以a≤-2(9分)
综上所述,实数a的取值范围是(-∞,-2]∪[1,2). ((10分))
点评 本题考查了不等式的解法、不等式的解集与判别式的关系、复合命题真假的判定方法、函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 坐标系与参数方程 | 不等式选讲 | |||
| 人数及均分 | 人数 | 均分 | 人数 | 均分 |
| 男同学 | 14 | 8 | 6 | 7 |
| 女同学 | 8 | 6.5 | 12 | 5.5 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | 3 | C. | $\frac{24}{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
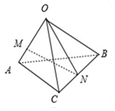 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {0,1,2,3} | C. | {3} | D. | {0,1,2,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com