
分析 利用坐标原点O到直线$\sqrt{2}$ax+by-1=0(a,b∈R)的距离为$\frac{{\sqrt{2}}}{2}$,得出$\frac{1}{\sqrt{2{a}^{2}+{b}^{2}}}$=$\frac{{\sqrt{2}}}{2}$,即2a2+b2=2,由|QP|2=a2+(b+1)2=$\frac{1}{2}$(b+2)2≤$\frac{1}{2}$($\sqrt{2}$+2)2,即可求出|QP|的最大值.
解答 解:∵坐标原点O到直线$\sqrt{2}$ax+by-1=0(a,b∈R)的距离为$\frac{{\sqrt{2}}}{2}$,
∴$\frac{1}{\sqrt{2{a}^{2}+{b}^{2}}}$=$\frac{{\sqrt{2}}}{2}$,
∴2a2+b2=2,
|QP|2=a2+(b+1)2=$\frac{1}{2}$(b+2)2≤$\frac{1}{2}$($\sqrt{2}$+2)2,∴|QP|的最大值为$\sqrt{2}$+1,
故答案为$\sqrt{2}$+1.
点评 本题考查点与直线距离公式的运用,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
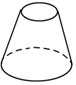 如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )
如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )| A. | 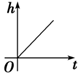 | B. | 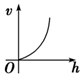 | C. | 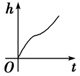 | D. | 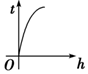 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (1,2]∪[3,+∞) | C. | [3,+∞) | D. | (0,2]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
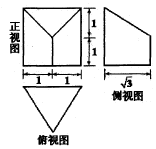
| A. | $2\sqrt{3}$ | B. | $\frac{{5\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com