
| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,π),sinx=tanx | |
| B. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$则p是q的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | D. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{5}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
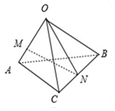 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
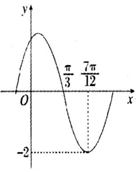 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
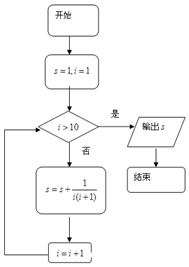
| A. | $\frac{5}{11}$ | B. | $\frac{21}{11}$ | C. | $\frac{13}{9}$ | D. | $\frac{17}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com