
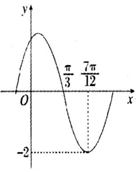
 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
分析 由函数的最值求出A,由周期求出ω,由图象经过定点($\frac{π}{3}$,0),求出φ的值,从而求得函数的解析式,利用三角函数的图象和性质逐一分析各个选项即可得解.
解答 解:由图象可知,A=2,$\frac{1}{4}$T=$\frac{7π}{12}$-$\frac{π}{3}$,则T=π.故①正确,
又由于ω=$\frac{2π}{T}$,则ω=2,
故f(x)=2sin(2x+φ).
由题中图象可知,f($\frac{π}{3}$)=2sin(2×$\frac{π}{3}$+φ)=0,则$\frac{2π}{3}$+φ=kπ,k∈z,
即 φ=kπ-$\frac{2π}{3}$,k∈z.
又因为|φ|<$\frac{π}{2}$,则 φ=$\frac{π}{3}$,
所以函数解析式为f(x)=2sin(2x+$\frac{π}{3}$),
对于②:由于f(0)=2sin$\frac{π}{3}$=$\sqrt{3}$,故②错误,
对于③:$y=f({x-\frac{π}{6}})$=2sin[2(x-$\frac{π}{6}$)+$\frac{π}{3}$]=2sin2x,为奇函数,故③错误,
对于④:由于:f($\frac{12π}{11}$)=2sin(2×$\frac{12π}{11}$+$\frac{π}{3}$)=2sin$\frac{83π}{33}$=2sin$\frac{17π}{33}$=2cos$\frac{0.5π}{33}$,f($\frac{14π}{13}$)=2sin(2×$\frac{14π}{13}$+$\frac{π}{3}$)=2sin$\frac{19π}{39}$=2cos$\frac{0.5π}{39}$,
又由于:$\frac{π}{2}$>$\frac{0.5π}{33}$>$\frac{0.5π}{39}$>0,
所以:cos$\frac{0.5π}{33}$<cos$\frac{0.5π}{39}$,可得$f({\frac{12π}{11}})<f({\frac{14π}{13}})$正确,
对于⑤:用特值法,当x=$\frac{π}{3}$时,f($\frac{π}{3}$)+f($\frac{4π}{3}$-$\frac{π}{3}$)=0+f(π)=0+2sin$\frac{π}{3}$=$\sqrt{3}$,故错误.
故选:D.
点评 本题主要考查y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,考查了三角函数的图象和性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{6}$,3-2$\sqrt{2}$) | B. | ($\frac{1}{6}$,$\frac{3}{2}$) | C. | (-∞,3-2$\sqrt{2}$) | D. | (3-2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{21}{2}$ | B. | $\frac{32}{3}$ | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
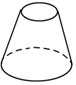 如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )
如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )| A. | 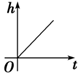 | B. | 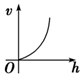 | C. | 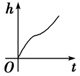 | D. | 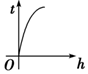 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com