
| A. | ($\frac{1}{6}$,3-2$\sqrt{2}$) | B. | ($\frac{1}{6}$,$\frac{3}{2}$) | C. | (-∞,3-2$\sqrt{2}$) | D. | (3-2$\sqrt{2}$,+∞) |
分析 利用函数g(x)=f(x)-ax,恰有三个不同的零点,推出函数f(x)与y=ax有3个交点,转化为直线y=ax与f(x)=x2+3x+2,x≤a有2个交点,与f(x)=$\frac{1}{6}x+2$,x>a有1个交点,列出不等式求解即可.
解答 解:函数g(x)=f(x)-ax,恰有三个不同的零点,就是函数f(x)与y=ax有3个交点,也就是函数y=ax与f(x)=x2+3x+2,x≤a的图象有2个交点,y=ax与f(x)=$\frac{1}{6}x+2$,x>a的图象有1个交点,
画出函数f(x)与y=ax的图象如图,
函数y=ax,看做直线斜率为a,由图象可知a$>\frac{1}{6}$,a小于直线与抛物线相切时的斜率,
可得$\left\{\begin{array}{l}{y=ax}\\{y={x}^{2}+3x+2}\end{array}\right.$,可得x2+(3-a)x+2=0,△=(3-a)2-8=0,解得a=3-2$\sqrt{2}$.
综上a∈($\frac{1}{6}$,3-2$\sqrt{2}$).
故选:A.
点评 本题考查函数的零点个数的求法与应用,考查数形结合以及分析问题解决问题的能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,π),sinx=tanx | |
| B. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$则p是q的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $\frac{17}{3}$ | C. | $\frac{20}{3}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
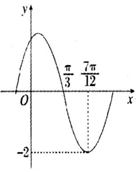 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com