
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅱ)问题等价于f(x)min>g(x)max,x∈[1,e],通过讨论a的范围,集合函数的单调性求出a的具体范围即可.
解答 解:(Ⅰ)g′(x)=$\frac{{x}^{2}-a}{{x}^{2}}$,(x≠0),
①a≤0时,g′(x)>0恒成立,
于是g(x)的递增区间是(-∞,0)和(0,+∞);
②a>0时,由g′(x)>0,解得:x<-$\sqrt{a}$或x>$\sqrt{a}$,
由g′(x)<0,解得:-$\sqrt{a}$<x<0或0<x<$\sqrt{a}$,
故g(x)在(-∞,-$\sqrt{a}$),($\sqrt{a}$,+∞)递增,在(-$\sqrt{a}$,0),(0,$\sqrt{a}$)递减,
综上,a≤0时,g(x)在(-∞,0)和(0,+∞)递增,
a>0时,g(x)在(-∞,-$\sqrt{a}$),($\sqrt{a}$,+∞)递增,在(-$\sqrt{a}$,0),(0,$\sqrt{a}$)递减;
(Ⅱ)a>0时,对于任意x1,x2∈[1,e]时,不等式f(x1)-g(x2)>0恒成立,
等价于f(x)min>g(x)max,x∈[1,e],
∵a>0,∴f(x)=alnx+2a在[1,e]递增,
∴f(x)min=f(1)=2a;
由(Ⅰ)得,
①当$\sqrt{a}$≥e,即a≥e2时,g(x)在[1,e]递减,
g(x)max=g(1)=1+a,2a>1+a,∴a>1;
故a≥e2时,f(x)min>g(x)max,x∈[1,e]成立,
②1≤$\sqrt{a}$<e时,g(x)max=max{g(1),g(e)},
当e≤a<e2时,g(1)>g(e),g(x)max=g(1)=1+a,
2a>1+a,∴a>1,
故e≤a<e2时,f(x)min>g(x)max,x∈[1,e]成立,
当1≤a<e时,g(x)max=g(e)=e+$\frac{a}{e}$,
2a>e+$\frac{a}{e}$,得a>$\frac{{e}^{2}}{2e-1}$,又1≤a<e,
故$\frac{{e}^{2}}{2e-1}$<a<e时,f(x)min>g(x)max,x∈[1,e]成立;
③当$\sqrt{a}$≤1,即0<a≤1时,g(x)max=g(e)=e+$\frac{a}{e}$,
2a>e+$\frac{a}{e}$,得a>$\frac{{e}^{2}}{2e-1}$与0<a≤1矛盾,
综上,存在实数a∈($\frac{{e}^{2}}{2e-1}$,+∞)时,对于任意x1,x2∈[1,e]时,不等式f(x1)-g(x2)>0恒成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{6}$,3-2$\sqrt{2}$) | B. | ($\frac{1}{6}$,$\frac{3}{2}$) | C. | (-∞,3-2$\sqrt{2}$) | D. | (3-2$\sqrt{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 等边三角形 | ||
| C. | 直角非等腰三角形 | D. | 等腰非直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-3或x>0} | B. | {x|x≤3或x≥0} | C. | {x|-3<x<0} | D. | {x|-3≤x≤0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.
某企业拟用10万元投资甲、乙两种商品.已知各投入x万元,甲、乙两种商品分别可获得y1,y2万元的利润,利润曲线${P_1}:{y_1}=a{x^n}$,P2:y2=bx+c,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
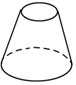 如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )
如图,向一个圆台型容器(下底比上底口径宽)匀速注水(单位时间注水体积相同),注满为止,设已注入的水体积为v,高度为h,时间为t,则下列反应变化趋势的图象正确的是( )| A. | 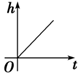 | B. | 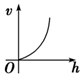 | C. | 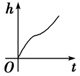 | D. | 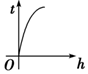 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com