
分析 (1)利用椭圆的离心率以及椭圆结果的点,求出长半轴与短半轴的长,即可得到椭圆方程;
(2)求出kAPkBP=-$\frac{1}{2}$,设直线MN的方程为x=my+t,代入椭圆方程,利用kOMkON=-$\frac{1}{2}$,推出t2=2m2+4,利用三角形的面积公式,化简求解即可推出结论.
解答 (1)解:椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(2,$\sqrt{2}$)且离心率等于$\frac{\sqrt{2}}{2}$,
可得$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,即:$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$,$\frac{4}{{a}^{2}}+\frac{2}{{b}^{2}}=1$,解得a2=8,b2=4,
所求椭圆方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
(2)证明:由题意M,N是椭圆C上非顶点的两点,
且AP∥OM,BP∥ON,设P(2$\sqrt{2}$cosθ,2sinθ)
则直线AP,BP斜率必存在且不为0,
又由已知kAPkBP=$\frac{2sinθ}{2\sqrt{2}cosθ+2\sqrt{2}}•\frac{2sinθ}{2\sqrt{2}cosθ-2\sqrt{2}}$=$\frac{4si{n}^{2}θ}{8(co{s}^{2}θ-1)}$=$-\frac{1}{2}$.
因为AP∥OM,BP∥ON,所以kOMkON=$-\frac{1}{2}$
设直线MN的方程为x=my+t,代入椭圆方程$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$,
得(2+m2)y2+2mty+t2-8=0…①,
设M,N的坐标分别为M(x1,y1),N(x2,y2),
则y1+y2=-$\frac{2mt}{2+{m}^{2}}$,y1y2=$\frac{{t}^{2}-8}{2+{m}^{2}}$,x1x2=
m2y1y2+mt(y1+y2)+t2=$\frac{2{t}^{2}-8{m}^{2}}{2+{m}^{2}}$,
所以kOMkON=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=$\frac{\frac{{t}^{2}-8}{2+{m}^{2}}}{\frac{2{t}^{2}-8{m}^{2}}{2+{m}^{2}}}$=-$\frac{1}{2}$,得t2=2m2+4,
又S△MON=$\frac{1}{2}$|t||y1-y2|=$\frac{1}{2}|t|\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{1}{2}|t|\sqrt{(\frac{2mt}{2+{m}^{2}})^{2}-4•\frac{{t}^{2}-8}{2+{m}^{2}}}$=$\frac{1}{2}\sqrt{{t}^{2}•(\frac{4{m}^{2}{t}^{2}}{\frac{1}{4}{t}^{4}}-4×\frac{{t}^{2}-8}{\frac{1}{2}{t}^{2}})}$=$\frac{1}{2}\sqrt{32}$=2$\sqrt{2}$,
即△MON的面积为定值2$\sqrt{2}$…(12分)
点评 本题考查椭圆的简单性质以及椭圆方程的求法,考查直线与椭圆的位置关系,考查斜率、面积的计算,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
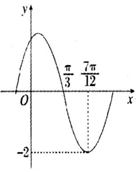 函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:
函数$f(x)=Asin({ωx+φ})({A>0,ω>0,|φ|≤\frac{π}{2}})$的部分图象如图所示,其中$f({\frac{π}{3}})=0,f({\frac{7π}{12}})=-2$,给出下列结论:| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -144 | B. | -120 | C. | -80 | D. | -60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com