
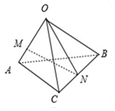
 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示) 分析 利用向量的三角形法则、平行四边形法则即可得出:$\overrightarrow{MN}$=$\overrightarrow{ON}-\overrightarrow{OM}$=$\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$-$\frac{2}{3}\overrightarrow{OA}$.
解答 解:$\overrightarrow{MN}$=$\overrightarrow{ON}-\overrightarrow{OM}$=$\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$-$\frac{2}{3}\overrightarrow{OA}$=$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.
故答案为:$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.
点评 本题考查了向量的三角形法则、平行四边形法则,考查了推理能力与计算能力,属于基础题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y-1=0 | B. | 2x-y-2=0 | C. | x-$\sqrt{3}$y-1=0 | D. | $\sqrt{3}$x-y-$\sqrt{3}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“2≥1”是假命题 | |
| B. | 命题“?x∈R,x2+1>0”的否定是:$?{x_0}∈R,{x_0}^2+1$<0 | |
| C. | 命题“若2a>2b,则a>b”的否命题是“若2a>2b,则a≤b” | |
| D. | “x>1”是“x2+x+2>0”充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,3] | B. | (1,2]∪[3,+∞) | C. | [3,+∞) | D. | (0,2]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com