
分析 (1)同椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,直线方程为y=x+1,联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=x+1}\end{array}\right.$,得7x2+8x-8=0,由此利用根的判别式,韦达定理、弦长公式能求出CD的长.
(2)当直线l无斜率时,直线方程为x=-1,|S1-S2|=0,当直线l斜率存在时,设直线方程为y=k(x+1)(k≠0),联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x+1)}\end{array}\right.$,得(3+4k2)x2+8k2x+4k2-12=0,由此利用根的判别式,韦达定理、弦长公式,结合已知条件能求出|S1-S2|的最大值.
解答 解:(1)因为F(-1,0)为椭圆的焦点,所以c=1,又b2=3,
所以a2=4,所以椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,
因为直线的倾斜角为45°,所以直线的斜率为1,
所以直线方程为y=x+1,和椭圆方程联立得到
$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=x+1}\end{array}\right.$,消掉y,得到7x2+8x-8=0,
所以△=288,x1+x2=-$\frac{8}{7}$,x1x2=-$\frac{8}{7}$,
所以线段CD的长|CD|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{2}$×$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{24}{7}$.
(2)当直线l无斜率时,直线方程为x=-1,
此时D(-1,$\frac{3}{2}$),C(-1,-$\frac{3}{2}$),△ABD,△ABC面积相等,|S1-S2|=0,
当直线l斜率存在(由题意知k≠0)时,设直线方程为y=k(x+1)(k≠0),
设C(x1,y1),D(x2,y2),
和椭圆方程联立得到$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x+1)}\end{array}\right.$,消掉y得(3+4k2)x2+8k2x+4k2-12=0,
△>0,方程有根,且x1+x2=-$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
此时|S1-S2|=2||y1|-|y2||=2|y1+y2|=2|k(x2+1)+k(x1+1)|
=2|k(x2+x1)+2k|=$\frac{12|k|}{3+4{k}^{2}}$=$\frac{12}{\frac{3}{|k|}+4|k|}$≤$\frac{12}{2\sqrt{\frac{3}{|k|}+4|k|}}$=$\frac{12}{2\sqrt{12}}$=$\sqrt{3}$(k=±$\frac{\sqrt{3}}{2}$时等号成立)
所以|S1-S2|的最大值为$\sqrt{3}$.
点评 本题考查线段长的求法,考查两三角形面积差的绝对值的最大值的求法,是中档题,解题时要认真审题,注意根的判别式,韦达定理、弦长公式、椭圆性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{5}$ | B. | 3 | C. | $\frac{24}{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
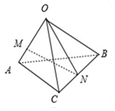 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BC}$ | B. | $3\overrightarrow{DF}$ | C. | $\overrightarrow{BF}$ | D. | $\frac{3}{2}\overrightarrow{BF}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用前卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米与75微克/立方米之间的空气质量为二级;在75微克/立方米以上的空气质量为超标.为了解甲,乙两座城市2016年的空气质量情况,从全年每天的PM2.5监测数据中随机抽取20天的数据作为样本,监测值如以下茎叶图所示(十位为茎,个位为叶).
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用前卫组织设定的最宽限值,即PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米与75微克/立方米之间的空气质量为二级;在75微克/立方米以上的空气质量为超标.为了解甲,乙两座城市2016年的空气质量情况,从全年每天的PM2.5监测数据中随机抽取20天的数据作为样本,监测值如以下茎叶图所示(十位为茎,个位为叶).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com