
分析 (1)利用等差数列的首项与公差通过数列的和求出a3,利用2a2,a6,a8+1成公比大于1的等比数列.求出公差,然后求解数列的通项公式.
(2)化简数列的通项公式,利用错位相减法求解数列的和即可.
解答 解:(1)设等差数列{an}的首项为a1,公差为d,S5=15,所以a3=3,2a2,a6,a8+1成公比大于1的等比数列.所以a62=2a2(a8+1),即:(a3+3d)2=2(a3+d)(a3+5d+1),所以d=1或d=$-\frac{15}{19}$(舍去),
所以a1=a3-2d=3-2=1.
所以an=n,
数列{an}的通项公式为:an=n;
(2)由(1)可知:设${b_n}={2^n}•{a_n}$=n•2n,
Tn=1×2+2×22+3×23+…+n•2n…①;
①×2可得:2Tn=1×22+2×23+3×24+…+(n-1)2n+n•2n+1…②,
①-②得:-Tn=2+22+23+…+2n-n•2n+1=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1=2n+1-2-n•2n+1.
∴Tn=(n-1)2n+1+2.
点评 本题考查数列求和,数列通项公式的应用,考查计算能力.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
| 坐标系与参数方程 | 不等式选讲 | |||
| 人数及均分 | 人数 | 均分 | 人数 | 均分 |
| 男同学 | 14 | 8 | 6 | 7 |
| 女同学 | 8 | 6.5 | 12 | 5.5 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,π),sinx=tanx | |
| B. | “?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 条件p:$\left\{\begin{array}{l}{x+y>4}\\{xy>4}\end{array}\right.$,条件q:$\left\{\begin{array}{l}{x>2}\\{y>2}\end{array}\right.$则p是q的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
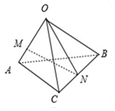 如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)
如图,空间四边形OACB中,$\overrightarrow{{O}{A}}$=$\overrightarrow{a}$,$\overrightarrow{{O}{B}}$=$\overrightarrow{b}$,$\overrightarrow{{O}C}$=$\overrightarrow{c}$,点M在OA上,且$\overrightarrow{OM}=\frac{2}{3}\overrightarrow{OA}$,点N为BC中点,则$\overrightarrow{MN}$等于$-\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}$.(用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com