Question

3．在正方形ABCD中，AB=AD=2，M，N分别是边BC，CD上的动点，当|$\overrightarrow{AM}$|•|$\overrightarrow{AN}$|=4时，则|$\overrightarrow{MN}$|的取值范围是$[\sqrt{2}，2]$．

Answer 1

分析 由题意画出图形，由$\overrightarrow{AM}•\overrightarrow{AN}$=4，得x+y=2．再由|$\overrightarrow{MN}$|=$\sqrt{（x-2）^{2}+（y-2）^{2}}$的几何意义，即线段x+y=2（0≤x≤2，0≤y≤2）上的动点到定点（2，2）的距离求解．

解答 解：如图，以A为原点建立平面直角坐标系，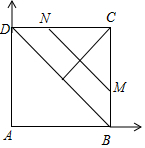

设M（2，y），N（x，2）（0≤x≤2，0≤y≤2），
则$\overrightarrow{AM}•\overrightarrow{AN}$=2x+2y=4，即x+y=2．
∴|$\overrightarrow{MN}$|=$\sqrt{（x-2）^{2}+（y-2）^{2}}$．
可以看做线段x+y=2（0≤x≤2，0≤y≤2）上的动点到定点（2，2）的距离．
最小值为$\sqrt{2}$，最大值为2．
故答案为：$[\sqrt{2}，2]$．

点评 本题考查了数量积运算性质，考查数形结合的解题思想方法与数学转化思想方法，属于中档题．