考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)使函数f(x)有意义即可求得f(x)的定义域为[-1,0)∪[1,+∞);
(2)设
f1(x)=x-,f2(x)=1-,通过求导,容易判断函数f(x)在[-1,0),[1,+∞)上单调递增,所以根据已知条件记得f(x)在[-1,0),[1,+∞)上单调递增,根据单调性即可求得f(x)的值域[0,+∞);
(3)由(1)(2)即可知道x
0≥1,并得到方程
x0=+,通过两边平方去根号的方法解该方程即可.
解答:
解:(1)要使f(x)有意义,则:
,解得:
-1≤x<0,或x≥1;
∴f(x)的定义域为[-1,0)∪[1,+∞);
(2)设
f1(x)=x-,
f2(x)=1-;
∴
f′1(x)=1+>0,f′2(x)=>0;
∴f
1(x),f
2(x)在[-1,0),和[1,+∞)上都为增函数;
∴根据已知条件知,f(x)在[-1,0),[1,+∞)上为增函数;
∵x∈[-1,0),x趋向0时,
-趋向正无穷,∴f(x)趋向正无穷;x∈[1,+∞),x趋向正无穷时,x趋向正无穷,∴f(x)趋向正无穷;
∴f(x)≥
,或f(x)≥0;
∴f(x)≥0;
∴f(x)的值域为[0,+∞);
(3)根据f(x)的定义域和值域,知x
0≥1;
x0=+;
∴
x0-=,两边平方并整理得:
x02-x0+1=2,两边平方并整理得,
(x02-x0-1)2=0;
∴
x02-x0-1=0,x
0≥1;
∴解得
x0=.
点评:考查函数定义域、值域的定义及求法,函数导数符号和函数单调性的关系,根据函数的单调性求函数的值域,以及两边平方去根号的方法解无理方程.



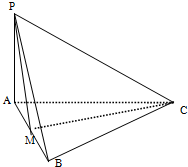 如图所示,PA⊥平面ABC,PA=AB,AB⊥BC,M为AB中点.
如图所示,PA⊥平面ABC,PA=AB,AB⊥BC,M为AB中点.