
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\sqrt{6}$ |
分析 由题意可得x1,x2为x2-3ax+2a2=0的解,运用韦达定理,可得a(x1+x2)+$\frac{1}{{x}_{1}{x}_{2}}$=3a2+$\frac{1}{2{a}^{2}}$,再由基本不等式即可得到所求最小值.
解答 解:关于x的一元二次不等式x2-3ax+2a2≥0的解集是(-∞,x1]∪[x2,+∞)(x1≠x2),
可得x1,x2为x2-3ax+2a2=0的解,
即有x1+x2=3a,x1x2=2a2,
则a(x1+x2)+$\frac{1}{{x}_{1}{x}_{2}}$=3a2+$\frac{1}{2{a}^{2}}$≥2$\sqrt{3{a}^{2}•\frac{1}{2{a}^{2}}}$=$\sqrt{6}$,
当且仅当3a2=$\frac{1}{2{a}^{2}}$时,上式取得最小值$\sqrt{6}$.
故选:D.
点评 本题考查二次不等式和二次方程的关系,注意运用韦达定理,考查基本不等式的运用:求最值,考查运算能力,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
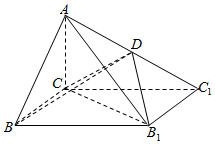 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com