
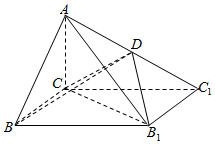
 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.分析 (Ⅰ)连结BC1交B1C于E,连结DE,由三角形中位线定理可得DE∥AB,再由线面平行的判定可得AB∥平面CDB1;
(Ⅱ)(1)由AC⊥平面BCC1B1,得BC⊥AC,再由线面垂直的判定可得BC⊥平面ACC1,进一步得到BC⊥CD,然后求解直角三角形可得$BD=\sqrt{2}$;
(2)依题意知AC、BC、CC1两两互相垂直,以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系如图示,求出平面ABB1 的一个法向量,则B1D与平面ABB1所成的角的正弦值可求.
解答 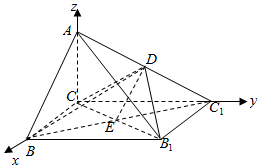 解:(Ⅰ)证明:连结BC1交B1C于E,连结DE,
解:(Ⅰ)证明:连结BC1交B1C于E,连结DE,
∵D、E分别为AC1和BC1的中点,
∴DE∥AB,
又∵DE?平面CDB1,AB?平面CDB1,
∴AB∥平面CDB1;
(Ⅱ)(1)∵AC⊥平面BCC1B1,BC?平面BCC1B1,
∴BC⊥AC,
又∵BC⊥CC1,AC∩CC1=C,
∴BC⊥平面ACC1,
∵CD?平面ACC1,
∴BC⊥CD,
在Rt△BCD,∵BC=1,$CD=\frac{1}{2}A{C_1}=\frac{1}{2}\sqrt{A{C^2}+{C_1}{C^2}}=1$,
∴$BD=\sqrt{2}$;
(2)依题意知AC、BC、CC1两两互相垂直,
以C为原点,CB所在的直线为x轴、CC1为y轴建立空间直角坐标系如图示,
得B(1,0,0),${B_1}(1,\sqrt{3},0)$,${C_1}(0,\sqrt{3},0),A(0,0,1)$,$D(0,\frac{{\sqrt{3}}}{2},\frac{1}{2})$,
故$\overrightarrow{{B_1}D}=(-1,-\frac{{\sqrt{3}}}{2},\frac{1}{2})$,$\overrightarrow{AB}=(1,0,-1)$,$\overrightarrow{B{B_1}}=(0,\sqrt{3},0)$,
设平面ABB1 的一个法向量为$\overrightarrow m=(a,b,c)$,
由$\overrightarrow m⊥\overrightarrow{AB},\overrightarrow m⊥\overrightarrow{B{B_1}}$,得$\left\{\begin{array}{l}a-c=0\\ \sqrt{3}b=0.\end{array}\right.$,令c=1,得$\overrightarrow m=(1,0,1)$,
设B1D与平面ABB1所成的角为θ,则$sinθ=\frac{{|\overrightarrow{{B_1}D}•\overrightarrow m|}}{{|\overrightarrow{{B_1}D}||\overrightarrow m|}}$=$|\frac{{-1+\frac{1}{2}}}{{\sqrt{2}•\sqrt{2}}}|=\frac{1}{4}$,
即B1D与平面ABB1 所成的角的正弦值为$\frac{1}{4}$.
点评 本题考查线面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求解线面角,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | y=-$\frac{1}{x}$ | B. | y=x3+x | C. | y=-x|x| | D. | y=ln$\frac{1+x}{1-x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,利用随机模拟方法计算阴影部分面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1+1,b=4b1,试验进行100次,前98次中落在阴影部分内的样本点数为40,且最后两次试验的随机数为a1=0.5,b1=0.3及a1=0.2,b1=0.6,那么本次模拟得出的面积约为1.64.
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,利用随机模拟方法计算阴影部分面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1+1,b=4b1,试验进行100次,前98次中落在阴影部分内的样本点数为40,且最后两次试验的随机数为a1=0.5,b1=0.3及a1=0.2,b1=0.6,那么本次模拟得出的面积约为1.64.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2\sqrt{6}}{3}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.1358 | B. | 0.1359 | C. | 0.2716 | D. | 0.2718 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为π的偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com