练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．函数y=2cos2（x+$\frac{3π}{4}$）-1是（　　）
    A．最小正周期为π的奇函数B．最小正周期为$\frac{π}{2}$的奇函数
    C．最小正周期为$\frac{π}{2}$的偶函数D．最小正周期为π的偶函数

    分析 先利用二倍角的余弦函数公式，诱导公式化简，进而利用周期公式和正弦函数的图象和性质即可得解．

    解答 解：∵y=2cos2（x+$\frac{3π}{4}$）-1=1+cos（2x+$\frac{3π}{2}$）-1=cos（2x+$\frac{3π}{2}$）=sin2x，
    ∴最小正周期为T=$\frac{2π}{2}$=π，利用正弦函数的图象和性质可知函数为最小正周期为π的奇函数．
    故选：A．

    点评 本题主要考查了二倍角的余弦函数公式，诱导公式，周期公式和正弦函数的图象和性质的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

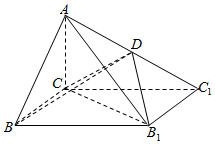    13．如图，已知四棱锥A-CBB1C1的底面为矩形，D为AC1的中点，AC⊥平面BCC1B1．
    （Ⅰ）证明：AB∥平面CDB1；
    （Ⅱ）若AC=BC=1，BB1=$\sqrt{3}$．
    （1）求BD的长；
    （2）求B1D与平面ABB1所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．设D为（x-2）2+y2=4的内部，计算$\underset{∬}{D}$y$\sqrt{{x}^{2}+{y}^{2}}$dσ=16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列结论正确的是（　　）
    A．“若a＞1，则a2＞a”的否命题是“若a＞1，则a2≤a”
    B．对于定义在R上的可导函数f（x），“f′（x0）=0”是“x0为极值点”的充要条件
    C．“若tanα$≠\sqrt{3}$，则$α≠\frac{π}{3}$”是真命题
    D．，?x0∈（-∞，0），使得3${\;}^{{x}_{0}}$＜4${\;}^{{x}_{0}}$成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．用0，1，2，3，4，5组成没有重复数字的五位数，比40000大的奇数共有（　　）
    A．72B．90C．120D．144

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知全集U=R，集合A={x|y=$\sqrt{1-x}$}，集合B={x|2x≤8}．
    （Ⅰ）求（∁UA）∩B；
    （Ⅱ）集合C={x|x＜a}，若“x∈C”是“x∈A”的充分不必要条件，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在一次诗词知识竞赛调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其中答对诗词名句与否的人数如图所示．
    （Ⅰ）完成下面的2×2列联表；判断是否有90%的把握认为答对诗词名句与年龄有关，请说明你的理由；（参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
    P（K2≥k0）0.100.050.0100.005
    k02.7063.8416.6357.879
    正确错误合计
    20～30
    30～40
    合计
    （Ⅱ）若计划在这次场外调查中按年龄段分层抽样选取6名选手，求3名选手中在20～30岁之间的人数的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在某化学反应的中间阶段，压力保持不变，温度从1℃变化到5℃，反应结果如表所示（t表示温度，y表示结果）：
    （1）判断变量t与y之间的正相关还是负相关，请用相关系数加以说明（精确到0.01）；
    （2）求化学反应的结果y对温度t的线性回归方程$\widehat{y}$=$\widehat{a}$+$\widehat{b}$t，并预测当温度到达10℃时反应结果为多少？
    t12345
    y3571011
    附：线性回归方程中$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$，$\widehat{b}$=$\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{ty}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$．
    相关系数r=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，$\sqrt{2}$=1.41，$\sqrt{3}$=1.73，$\sqrt{7}$=2.65．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若$\frac{|sinx|}{sinx}$+$\frac{cosx}{|cosx|}$+$\frac{|tanx|}{tanx}$=-1，则角x一定不是（　　）
    A．第四象限角B．第三象限角C．第二象限角D．第一象限角

    查看答案和解析>>

    同步练习册答案