
 如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,利用随机模拟方法计算阴影部分面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1+1,b=4b1,试验进行100次,前98次中落在阴影部分内的样本点数为40,且最后两次试验的随机数为a1=0.5,b1=0.3及a1=0.2,b1=0.6,那么本次模拟得出的面积约为1.64.
如图,点A的坐标为(1,0),点C的坐标为(2,4),函数f(x)=x2,利用随机模拟方法计算阴影部分面积时,利用计算器产生两组0~1之间的均匀随机数a1=RAND,b1=RAND,然后进行平移与伸缩变换a=a1+1,b=4b1,试验进行100次,前98次中落在阴影部分内的样本点数为40,且最后两次试验的随机数为a1=0.5,b1=0.3及a1=0.2,b1=0.6,那么本次模拟得出的面积约为1.64. 分析 由题意知本题是模拟方法估计概率,只须计算出总共100次试验,一共有多少次落在所求面积区域内,结合几何概型的计算公式即可求得.计算y=x2与y=4围成的面积它的几何意义是函数f(x)(其中0≤x≤2)的图象与x轴、直线x=0和直线x=2所围成图形的面积,也可由积分得到结果
解答 解:由a1=0.5,b1=0.3得a=1.5,b=1.2,(1.5,1.2)落在y=x2与y=4围成的区域内,
由a1=0.2,b1=0.6得:a=1.2,b=2.4,(1.2,2.4)落在y=x2与y=4围成的区域内
所以本次模拟得出的面积为4×$\frac{42}{100}$=1.64.
故答案为:1.64.
点评 本题考查了定积分的运用以及几何概型的概率的意义;关键是明确模拟得出的面积为矩形面积乘以阴影部分面积与矩形面积比.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4:5:6 | B. | 3:5:7 | C. | 4:6:8 | D. | 3:5:6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 21 | C. | 34 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
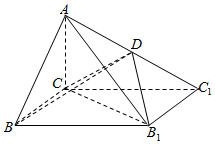 如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.
如图,已知四棱锥A-CBB1C1的底面为矩形,D为AC1的中点,AC⊥平面BCC1B1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.3 | C. | 0.4 | D. | 0.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com