练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，M、N分别是棱C1D1、C1C的中点．以下四个结论：
    ①直线AM与直线CC1相交；
    ②直线AM与直线BN平行；
    ③直线AM与直线DD1异面；
    ④直线BN与直线MB1异面．
    其中正确结论的序号为 ．
    （注：把你认为正确的结论序号都填上）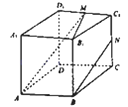

    【答案】③④
    【解析】∵直线CC1在平面CC1D1D上，
    而M∈平面CC1D1D，A平面CC1D1D，
    ∴直线AM与直线CC1异面，故①不正确，
    ∵直线AM与直线BN异面，故②不正确，
    ∵直线AM与直线DD1既不相交又不平行，
    ∴直线AM与直线DD1异面，故③正确，
    利用①的方法验证直线BN与直线MB1异面，故④正确，
    总上可知有两个命题是正确的，
    故答案为：③④
    利用两条直线是异面直线的判断方法来验证①③④的正误，②要证明两条直线平行，从图形上发现这两条直线也是异面关系，得到结论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

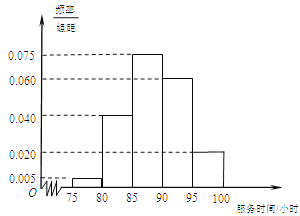
    【题目】某市规定，高中学生三年在校期间参加不少于小时的社区服务才合格．教育部门在全市随机抽取200位学生参加社区服务的数据，按时间段，，，

    ，（单位：小时）进行统计，其频率分布直方图如图所示．

    （Ⅰ）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计

    从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；

    （Ⅱ）从全市高中学生（人数很多）中任意选取3位学生，记为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】斜三棱柱ABC﹣A1B1C1中，AA1=AC=BC=2，∠A1AC=∠C1CB=60°，且平面ACC1A1⊥平面BCC1B1 ， 则A1B的长度为 ．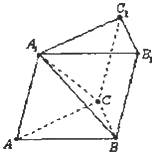

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数中，是偶函数且不存在零点的是（ ）
    A.y=x2
    B.y=
    C.y=log2x
    D.y=（ ）|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞3且a≠ ，命题p：指数函数f（x）=（2a﹣6）x在R上单调递减，命题q：关于x的方程x2﹣3ax+2a2+1=0的两个实根均大于3．若p或q为真，p且q为假，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：
    ①三点确定一个平面；
    ②在空间中，过直线外一点只能作一条直线与该直线平行；
    ③若平面α上有不共线的三点到平面β的距离相等，则α∥β；
    ④若直线a、b、c满足a⊥b、a⊥c，则b∥c．
    其中正确命题的个数是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知三棱锥的底面是直角三角形，直角边长分别为3和4，过直角顶点的侧棱长为4，且垂直于底面，该三棱锥的正视图是（ ）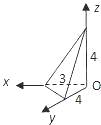
    A.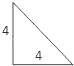
    B.
    C.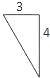
    D.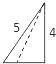

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合A={x|x2+x+p=0}．
    （Ⅰ）若A=，求实数p的取值范围；
    （Ⅱ）若A中的元素均为负数，求实数p的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆经过点，且离心率为.

    （1）求椭圆的方程；

    （2）设点在轴上的射影为点，过点的直线与椭圆相交于， 两点，且，求直线的方程.

    查看答案和解析>>

    同步练习册答案