
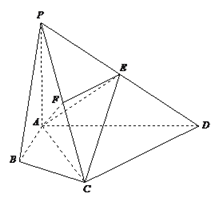
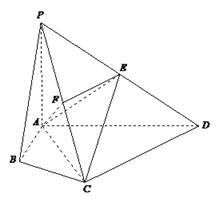
【题目】四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,
E为PD的中点,PA=2AB=2.
(1)若F为PC的中点,求证PC⊥平面AEF;
(2)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)由题意可证得AF⊥PC.EF⊥PC.利用线面垂直的判断定理可得PC⊥平面AEF.
(2)建立空间直角坐标系,结合半平面的法向量可得二面角![]() 的平面角的正弦值是
的平面角的正弦值是![]() .
.
试题解析:
(1)证明:∵PA=CA,F为PC的中点,
∴AF⊥PC. ∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,∴CD⊥平面PAC.∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC.∵AF∩EF=F,
∴PC⊥平面AEF.
(2)解:以点![]() 为坐标原点,直线
为坐标原点,直线![]() 分别为
分别为
![]() 轴和
轴和![]() 轴,建立空间直角坐标系。
轴,建立空间直角坐标系。
![]()
可求得平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,设二面角
,设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数(0,
有如下性质:如果常数t>0,那么该函数(0, ![]() ]上是减函数,在[
]上是减函数,在[ ![]() ,+∞)上是增函数.
,+∞)上是增函数.
(1)已知f(x)= ![]() ,g(x)=﹣x﹣2a,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
,g(x)=﹣x﹣2a,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
(2)对于(1)中的函数f(x)和函数g(x),若对于任意的x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂从工程设计B到试生产H的工序流程图,方框上方的数字为这项工序所用的天数,则从工程设计到结束试生产需要的最短时间为( )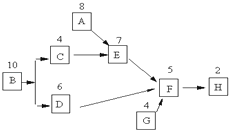
A.22天
B.23天
C.28天
D.以上都不对
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
已知直线l:ρsin(θ+![]() )=
)=![]() m,曲线C:
m,曲线C: 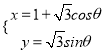
(1)当m=3时,判断直线l与曲线C的位置关系;
(2)若曲线C上存在到直线l的距离等于![]() 的点,求实数m的范围.
的点,求实数m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com