
【题目】几位大学生响应国家的创业号召,开发了一款面向中学生的应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。这款软件的激活码为下面数学题的答案:记集合![]() .例如:
.例如:![]() ,若将集合
,若将集合![]() 的各个元素之和设为该软件的激活码,则该激活码应为____________;
的各个元素之和设为该软件的激活码,则该激活码应为____________;
定义 现指定
现指定![]() ,将集合
,将集合![]() 的元素从小到大排列组成数列
的元素从小到大排列组成数列![]() ,若将
,若将![]() 的各项之和设为该软件的激活码,则该激活码应为_____________.
的各项之和设为该软件的激活码,则该激活码应为_____________.
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为a的正方体ABCD-A1B1C1D1中,E是棱DD1的中点:
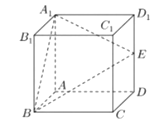
(1)求点D到平面A1BE的距离;
(2)在棱![]() 上是否存在一点F,使得B1F∥平面A1BE,若存在,指明点F的位置;若不存在,请说明理由。
上是否存在一点F,使得B1F∥平面A1BE,若存在,指明点F的位置;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上(不包括端点).
上(不包括端点).

(1)求证:![]()
(2)是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中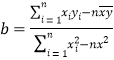 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
A. |OA|>|OB|B. |OA|<|OB|
C. |OA|=|OB|D. |OA|与|OB|大小关系不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com