
【题目】如图,已知![]() ,
,![]()
![]() ,且
,且![]() 是
是![]() 的中点,
的中点,![]() .
.
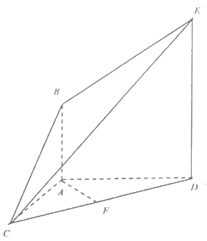
(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() 。
。
【解析】
(1)取![]() 的中点
的中点![]() ,可以利用中位线定理,根据已知的平行关系和长度关系,可以得到一个平行四边形,利用平行四边形的对边平行,这样得到线线平行,也就能证明出线面平行;
,可以利用中位线定理,根据已知的平行关系和长度关系,可以得到一个平行四边形,利用平行四边形的对边平行,这样得到线线平行,也就能证明出线面平行;
(2)通过已知和(1)可知![]() ,通过线面垂直和平行线的性质,可以
,通过线面垂直和平行线的性质,可以![]() 这样可以证明出线面垂直,而
这样可以证明出线面垂直,而![]() 从而证明出
从而证明出![]() 平面
平面![]() 利用面面垂直的判定定理可以证明出平面
利用面面垂直的判定定理可以证明出平面![]() 平面
平面![]() ;
;
(3)通过(2)证明出的线面垂直关系,找到线面角,利用勾股定理、平行四边形的性质,求出相关的边,利用正弦的定义,求出![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
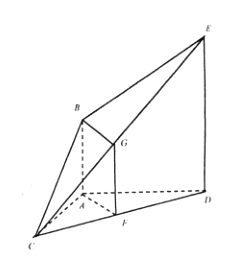
(1)如上图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
由![]() 是
是![]() 的中点,
的中点,![]() 且
且![]() 又
又![]() ,且
,且![]()
![]() 且
且![]() .
. ![]() 是平行四边形,从而
是平行四边形,从而![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 因此
, 因此![]() ;
;
(2)证明:![]() 是
是![]() 的中点,
的中点,![]() ,
,
因为![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]()
![]() 而
而![]()
![]() 平面
平面![]()
由![]() 可知
可知![]() 平面
平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(3)由(2)知![]() 平面
平面![]()
![]() 是
是![]() 在平面
在平面![]() 的射影,则
的射影,则![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,因为
,因为![]() ,所以
,所以![]() ,由(1)可知:
,由(1)可知:
![]() 是平行四边形,从而
是平行四边形,从而![]() ,
,
在![]() 中,
中,![]()
![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() 。
。


科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
说明你的理由;

(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款面向中学生的应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。这款软件的激活码为下面数学题的答案:记集合![]() .例如:
.例如:![]() ,若将集合
,若将集合![]() 的各个元素之和设为该软件的激活码,则该激活码应为____________;
的各个元素之和设为该软件的激活码,则该激活码应为____________;
定义 现指定
现指定![]() ,将集合
,将集合![]() 的元素从小到大排列组成数列
的元素从小到大排列组成数列![]() ,若将
,若将![]() 的各项之和设为该软件的激活码,则该激活码应为_____________.
的各项之和设为该软件的激活码,则该激活码应为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com