
【题目】已知函数![]() ,函数
,函数![]() .
.
(1)当![]() 时,若
时,若![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() 和
和![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.![]()
【解析】
(1)![]() ,由已知得
,由已知得![]() ,问题转化为
,问题转化为![]() ,
,![]() ,求
,求![]() ,通过判断
,通过判断![]() ,得出
,得出![]() 单调性,以及
单调性,以及![]() ,求出单调区间
,求出单调区间![]() 的极值,最值,进而求出结论;
的极值,最值,进而求出结论;
(2)![]() ,
,![]() ,
,![]() 时,
时,![]() ,至多一个零点,不成立;
,至多一个零点,不成立;![]() 时,求出单调区间,极值,分析
时,求出单调区间,极值,分析![]() 函数值的变化趋势,求得
函数值的变化趋势,求得![]() 由两个零点时,
由两个零点时,![]() ,
,![]() ,设
,设![]() ,并满足
,并满足![]() ,可得
,可得![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,要证
,要证![]() ,等价转化为证明
,等价转化为证明![]() ,设
,设![]() ,通过求导,再构造函数再求导,可证
,通过求导,再构造函数再求导,可证![]() 在
在![]() 上单增,即可证明结论.
上单增,即可证明结论.
(1)令![]() ,当
,当![]() 时,
时,![]() .
.
若![]() 对任意
对任意![]() 恒成立,即为
恒成立,即为![]()
∵![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
![]() 时,
时,![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() .
.
(2)![]() ,
,![]() ,
,
![]() 时,
时,![]() ,
,![]() 在
在![]() 上单增,至多一个零点,不成立;
上单增,至多一个零点,不成立;
![]() 时,由
时,由![]() 得
得![]() ,
,
![]() 在
在![]() 上单减,在
上单减,在![]() 上单增.
上单增.
![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
要存在两零点只需![]() ,即
,即![]() ,得
,得![]() .
.
不妨设![]() ,由
,由![]() 得
得![]() ,
,
令![]() ,则
,则![]() ,即
,即![]() ,而
,而
![]()
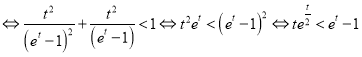 (*)
(*)
令![]() ,
,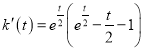 ,
,
令![]() ,
,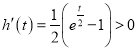 ,
,
∴![]() 在
在![]() 上单增,
上单增,![]() ,
,
∴![]() ,
,![]() 在
在![]() 上单增,
上单增,
![]() ,故(*)成立,得证.
,故(*)成立,得证.


科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款面向中学生的应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。这款软件的激活码为下面数学题的答案:记集合![]() .例如:
.例如:![]() ,若将集合
,若将集合![]() 的各个元素之和设为该软件的激活码,则该激活码应为____________;
的各个元素之和设为该软件的激活码,则该激活码应为____________;
定义 现指定
现指定![]() ,将集合
,将集合![]() 的元素从小到大排列组成数列
的元素从小到大排列组成数列![]() ,若将
,若将![]() 的各项之和设为该软件的激活码,则该激活码应为_____________.
的各项之和设为该软件的激活码,则该激活码应为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学图书馆举行高中志愿者检索图书的比赛,从高一、高二两个年级各抽取10名志愿者参赛。在规定时间内,他们检索到的图书册数的茎叶图如图所示,规定册数不小于20的为优秀.
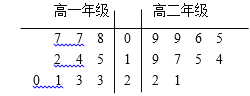
(Ⅰ) 从两个年级的参赛志愿者中各抽取两人,求抽取的4人中至少一人优秀的概率;
(Ⅱ) 从高一10名志愿者中抽取一人,高二10名志愿者中抽取两人,3人中优秀人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调等比数列![]() 中,首项为
中,首项为 ![]() ,其前n项和是
,其前n项和是![]() ,且
,且![]() 成等差数列,数列
成等差数列,数列![]() 满足条件
满足条件![]()
(Ⅰ) 求数列![]() 、
、![]() 的通项公式;
的通项公式;
(Ⅱ) 设 ![]() ,记数列
,记数列![]() 的前
的前![]() 项和
项和 ![]() .
.
①求 ![]() ;②求正整数
;②求正整数![]() ,使得对任意
,使得对任意![]() ,均有
,均有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆柱![]() 的底面圆
的底面圆![]() 的半径
的半径![]() ,圆柱的表面积为
,圆柱的表面积为![]() ;点
;点![]() 在底面圆
在底面圆![]() 上,且直线
上,且直线![]() 与下底面所成的角的大小为
与下底面所成的角的大小为![]() ,
,

(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求二面角![]() 的大小(结果用反三角函数值表示).
的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
某学校高一数学兴趣小组对学生每周平均体育锻炼小时数与体育成绩优秀(体育成绩满分100分,不低于85分称优秀)人数之间的关系进行分析研究,他们从本校初二,初三,高一,高二,高三年级各随机抽取了40名学生,记录并整理了这些学生周平均体育锻炼小时数与体育成绩优秀人数,得到如下数据表:
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均体育锻炼小时数工(单位:小时) | 14 | 11 | 13 | 12 | 9 |
体育成绩优秀人数y(单位:人) | 35 | 26 | 32 | 26 | 19 |
该兴趣小组确定的研究方案是:先从这5组数据中选取3组数据求线性回归方程,再用剩下的2组数据进行检验.
(1)若选取的是初三,高一,高二的3组数据,请根据这3组数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选取的检验数据的误差均不超过1,则认为得到的线性回归方程是可靠的,试问(1)中所得到的线性回归方程是否可靠?
参考数据:![]() ,
,![]() .
.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com