
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上(不包括端点).
上(不包括端点).

(1)求证:![]()
(2)是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() 是椭圆
是椭圆![]() 上的一点,从原点
上的一点,从原点![]() 向
向
圆![]() 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点![]() .
.

(1)若![]() 点在第一象限,且直线
点在第一象限,且直线![]() 互相垂直,求圆
互相垂直,求圆![]() 的方程;
的方程;
(2)若直线![]() 的斜率存在,并记为
的斜率存在,并记为![]() ,求
,求![]() 的值;
的值;
(3)试问![]() 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省确定从2021年开始,高考采用“![]() ”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取
”的模式,取消文理分科,即“3”包括语文、数学、外语,为必考科目;“1”表示从物理、历史中任选一门;“2”则是从生物、化学、地理、政治中选择两门,共计六门考试科目.某高中从高一年级2000名学生(其中女生900人)中,采用分层抽样的方法抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生110人,求
名学生中含男生110人,求![]() 的值及抽取到的女生人数;
的值及抽取到的女生人数;
(2)学校计划在高二上学期开设选修中的“物理”和“历史”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的n名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目).下表是根据调查结果得到的![]() 列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
列联表,请将列联表补充完整,并判断是否有99.5%的把握认为选择科目与性别有关?
说明你的理由;

(3)在(2)的条件下,从抽取的选择“物理”的学生中按分层抽样抽取6人,再从这6名学生中抽取2人,对“物理”的选课意向作深入了解,求2人中至少有1名女生的概率.
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题:(1)如果一个平面内有无数条直线平行于另一个平面,则这两个平面平行;(2)一个平面内的任意一条直线都与另一个平面不相交,则这两个平面平行;(3)一个平面内有不共线的三点到另一个平面的距离相等,则这两个平面平行;其中正确命题的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款面向中学生的应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动。这款软件的激活码为下面数学题的答案:记集合![]() .例如:
.例如:![]() ,若将集合
,若将集合![]() 的各个元素之和设为该软件的激活码,则该激活码应为____________;
的各个元素之和设为该软件的激活码,则该激活码应为____________;
定义 现指定
现指定![]() ,将集合
,将集合![]() 的元素从小到大排列组成数列
的元素从小到大排列组成数列![]() ,若将
,若将![]() 的各项之和设为该软件的激活码,则该激活码应为_____________.
的各项之和设为该软件的激活码,则该激活码应为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某种零件的一条生产线的生产过程,从生产线上随机抽取一批零件,根据其尺寸的数据得到如图所示的频率分布直方图.若尺寸落在区间(![]() )之外,则认为该零件属“不合格”的零件,其中
)之外,则认为该零件属“不合格”的零件,其中![]() ,分别为样本平均数和样本标准差,计算可得:
,分别为样本平均数和样本标准差,计算可得:![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).

(1)若一个零件的尺寸是![]() ,试判断该零件是否属于“不合格”的零件;
,试判断该零件是否属于“不合格”的零件;
(2)工厂利用分层抽样的方法从样本的前3组中抽出6个零件,标上记号,并从这6个零件中再抽取2个,求再次抽取的2个零件中恰有1个尺寸不超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学图书馆举行高中志愿者检索图书的比赛,从高一、高二两个年级各抽取10名志愿者参赛。在规定时间内,他们检索到的图书册数的茎叶图如图所示,规定册数不小于20的为优秀.
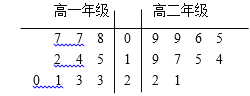
(Ⅰ) 从两个年级的参赛志愿者中各抽取两人,求抽取的4人中至少一人优秀的概率;
(Ⅱ) 从高一10名志愿者中抽取一人,高二10名志愿者中抽取两人,3人中优秀人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆柱![]() 的底面圆
的底面圆![]() 的半径
的半径![]() ,圆柱的表面积为
,圆柱的表面积为![]() ;点
;点![]() 在底面圆
在底面圆![]() 上,且直线
上,且直线![]() 与下底面所成的角的大小为
与下底面所成的角的大小为![]() ,
,

(1)求点![]() 到平面
到平面![]() 的距离;
的距离;
(2)求二面角![]() 的大小(结果用反三角函数值表示).
的大小(结果用反三角函数值表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com