
已知圆C:x2+(y-2)2=5,直线l:mx-y+1=0.
(1)求证:对m∈R,直线l与圆C总有两个不同交点;
(2)若圆C与直线相交于点A和点B,求弦AB的中点M的轨迹方程.
(1)证明:法一:直线系l:mx-y+1=0恒过定点(0,1),且点(0,1)在圆C:x2+(y-2)2=5内部,所以对m∈R,直线l与圆C总有两个不同交点.--------3分
法二:直线方程与圆的方程联立,消去y得(m2+1)x2-2mx-4=0,
∵Δ=4m2+16(m2+1)=20m2+16>0,∴对m∈R,直线l与圆C总有两个不同交点.
法三:圆心到直线的距离d=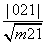 =
=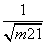 ≤1<
≤1<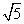 ,所以对m∈R,直线l与圆C总有两个不同交点.
,所以对m∈R,直线l与圆C总有两个不同交点.
(2)解:设A(x1,y1),B(x2,y2),M(x,y),
由方程(m2+1)x2-2mx-4=0,得x1+x2=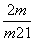 ,-
,-
∴x=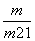 ,由mx-y+1=0,得m=
,由mx-y+1=0,得m=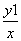 ,
,
代入x=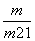 ,得x[(
,得x[(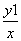 )2+1]=
)2+1]=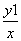 ,
,
化简得x2+(y-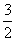 )2=
)2= . -
. -


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com