

| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
分析 由题意可知,三条侧棱两两垂直的正三棱锥是正四面体,要求该三棱锥左视图的面积,必须求出正四面体的高及底面三角形的高,从而解决问题
解答 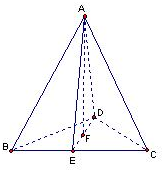 解:正三棱锥A-BCD的三条侧棱两两垂直,
解:正三棱锥A-BCD的三条侧棱两两垂直,
∴正三棱锥A-BCD是正四面体,
底面是边长为2正三角形,底面上的高是$\sqrt{3}$,
A到底面的距离:h=$\sqrt{{AD}^{2}-{DF}^{2}}$=$\frac{\sqrt{6}}{3}$;
∴该三棱锥的左视图的面积:S△ADE=$\frac{1}{2}$×DE×AF=$\frac{1}{2}$×$\sqrt{3}$×$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{2}}{2}$,
故选:C.
点评 本题考查三视图求面积,体积,空间想象能力,是基础题.


科目:高中数学 来源: 题型:解答题
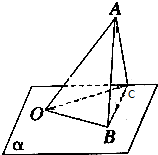 如图所示,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.
如图所示,已知∠BOC在平面α内,OA是平面α的斜线,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sinx | B. | y=|cosx| | C. | y=sin(2x-$\frac{π}{2}$) | D. | y=tan2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
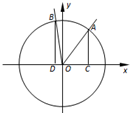 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3(结果保留一位小数).
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60)…[90,100]后画出如图频率分布直方图.观察图形的信息,回答下列问题:这次考试的中位数为73.3(结果保留一位小数).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com