
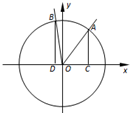
 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
分析 利用任意角的三角函数的定义求得S1,S2的值,再根据S1=$\frac{4}{3}$S2,求得tan2α的值,可得tanα的值.
解答 解:由题意可得S1 =$\frac{1}{2}$•cosα•sinα=$\frac{1}{4}$sin2α,S2 =$\frac{1}{2}$•[-cos($α+\frac{π}{4}$)]•sin(α+$\frac{π}{4}$)=-$\frac{1}{4}$sin(2α+$\frac{π}{2}$)=-$\frac{1}{4}$cos2α.
再根据S1=$\frac{4}{3}$S2,可得$\frac{1}{4}$•sin2α=$\frac{4}{3}$•(-$\frac{1}{4}$cos2α),∴tan2α=-$\frac{4}{3}$=$\frac{2tanα}{1{-tan}^{2}α}$,
求得tanα=2,或tanα=-$\frac{1}{2}$ (不满足α∈($\frac{π}{4}$,$\frac{π}{2}$),故舍去),
故选:B.
点评 本题主要考查任意角的三角函数的定义,二倍角公式的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-3=0 | B. | x+2y-4=0 | C. | x-y+3=0 | D. | x-2y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在梯形ABCD中,AD∥BC∥EF,E是AB的中点,F是CD的中点,EF交BD于G,交AC于H,若AD=5,BC=8,则GH=$\frac{3}{2}$.
如图,在梯形ABCD中,AD∥BC∥EF,E是AB的中点,F是CD的中点,EF交BD于G,交AC于H,若AD=5,BC=8,则GH=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com