
| A. | x+y-3=0 | B. | x+2y-4=0 | C. | x-y+3=0 | D. | x-2y-4=0 |
分析 本题常规思想是采用待定系数法,设直线l方程y=k(x-2)+1,表示出点A、B的坐标,根据直线过x轴、y轴正半轴,确定向量$\overrightarrow{PA}$与$\overrightarrow{PB}$方向相反,再利用数量积运算及基本不等式,求当|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|取到最小值时的参数k.
也可以用四个选项进行验证比较,①是否过P点,②直线的斜率是否为负,②|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|的值谁最小.
解答 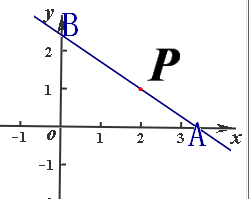 解法一:
解法一:
解:由题知,直线l的斜率存在且小于0,故设直线l的方程为y=k(x-2)+1,
令y=0,得x=$2-\frac{1}{k}$,
令x=0,得y=1-2k,
所以,A($2-\frac{1}{k}$,0),B(0,1-2k),
故 $\overrightarrow{PA}$=($-\frac{1}{k}$,-1),$\overrightarrow{PB}$=(-2,-2k),
又由题,及右图知向量$\overrightarrow{PA}$与$\overrightarrow{PB}$方向相反,
∴$\overrightarrow{PA}•\overrightarrow{PB}=|\overrightarrow{PA}||\overrightarrow{PB}|cos<\overrightarrow{PA},\overrightarrow{PB}>$=$-|\overrightarrow{PA}||\overrightarrow{PB}|$,
∴$|\overrightarrow{PA}||\overrightarrow{PB}|$=$-\overrightarrow{PA}•\overrightarrow{PB}$=$-(\frac{2}{k}+2k)$=$(-\frac{2}{k})+(-2k)$.
∵k<0
∴$-(\frac{2}{k}+2k)$=$(-\frac{2}{k})+(-2k)$ $≥2\sqrt{(-\frac{2}{k})•(-2k)}$=4.
当且仅当 k=-1时,取得 $|\overrightarrow{PA}||\overrightarrow{PB}|$的最小值4.
∴直线l的方程为:y=-(x-2)+1即x+y-3=0,
故选:A.
解法二:
解:由题,直线l交x,y正半轴于A,B两点,知直线l的斜率为负值,
C选项,斜率为1,故排除.
D选项,斜率为$\frac{1}{2}$,故排除.
A选项,斜率为-1,符合.
B选项,斜率为$-\frac{1}{2}$,符合.
故选项A、B进行下一步的筛选,
比较|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|的值,若值跟大,则排除,值更小,则是答案.
A选项:直线l与x轴、y轴的交点分别为A(3,0),B(0,3),
计算|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|=$\sqrt{(3-2)^{2}+(0-1)^{2}}$•$\sqrt{(0-2)^{2}+(3-1)^{2}}$=4,
B选项:直线l与x轴、y轴的交点分别为A(4,0),B(0,2)
计算|$\overrightarrow{PA}$|•|$\overrightarrow{PB}$|=$\sqrt{(4-2)^{2}+(0-1)^{2}}$•$\sqrt{(0-2)^{2}+(2-1)^{2}}$=5,
知 4<5.
故选:A.
点评 知识点考查了直线与向量的综合应用,向量的数量积与模积的关系,基本不等式;数学思想方法考查了数形结合、待定系数法、排除法、比较法.综合性虽然比较强,但考查的是常用知识点,没有设置易错点,故属于中档题.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sinx | B. | y=|cosx| | C. | y=sin(2x-$\frac{π}{2}$) | D. | y=tan2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
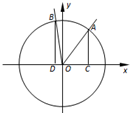 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?β,n?β,m∥α,n∥α,则α∥β | B. | 若m?α,m?β,α∥β,则m∥n | ||
| C. | 若α⊥β,m?α,n?β,则m⊥n | D. | 若m⊥α,n?α,则m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com