
分析 (1)a=1时,化简函数f(x),根据二次函数和三角函数的性质即可求出f(x)的最大、最小值与对应的x的值;
(2)化简函数f(x),讨论a的取值范围,利用二次函数的图象与性质,即可求出f(x)的最大值.
解答 解:(1)a=1时,函数f(x)=sin2x+cosx+5
=1-cos2x+cosx+5
=-${(cosx-\frac{1}{2})}^{2}$+$\frac{25}{4}$,
当cosx=$\frac{1}{2}$,即x=2kπ±$\frac{π}{3}$,k∈Z时,
函数f(x)取得最大值$\frac{25}{4}$,
当cosx=-1,即x=2kπ+π,k∈Z时,
函数f(x)取得最小值4;
(2)函数f(x)=sin2x+acosx+5
=1-cos2x+acosx+5
=-${(cosx-\frac{a}{2})}^{2}$+6+$\frac{{a}^{2}}{4}$,a∈R;
当a≤-2,即$\frac{a}{2}$≤-1时,f(x)在cosx=-1时取得最大值5-a;
当-2<a<2,即-1<$\frac{a}{2}$<1时,f(x)在cosx=$\frac{a}{2}$时取得最大值6+$\frac{{a}^{2}}{4}$;
当a≥2,即$\frac{a}{2}$≥1时,f(x)在cos=1时取得最大值5+a;
∴函数f(x)在R上的最大值为
g(a)=$\left\{\begin{array}{l}{5-a,a≤-2}\\{6+\frac{{a}^{2}}{4},-2<a<2}\\{5+a,a≥2}\end{array}\right.$.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了二次函数的图象与性质的应用问题,是综合性题目.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l1一定与l4垂直 | |
| B. | l1一定与l4平行 | |
| C. | l1一定与l4共面 | |
| D. | l1与l4的位置关系可能是平行,相交,或异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
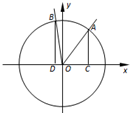 在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )
在平面直角坐标系xOy中,角α的顶点是坐标原点,始边为x轴的正半轴,终边与单位圆O交于点A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).将角α终边绕原点按逆时针方向旋转$\frac{π}{4}$,交单位圆于点B(x2,y2).过A,B作x轴的垂线,垂足分别为C,D,记△AOC及△BOD的面积分别为S1,S2,且S1=$\frac{4}{3}$S2,则tanα的值等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{4}{21}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
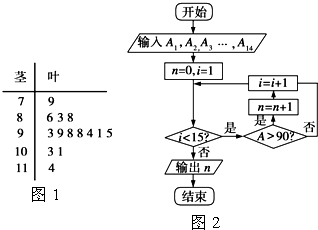 如图1是某高三学生进入高中-二年来的数学考试成绩茎叶图,第1次到第 14次.考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是10.
如图1是某高三学生进入高中-二年来的数学考试成绩茎叶图,第1次到第 14次.考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是10.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3cosx | B. | f(x)=x3+x2 | C. | f(x)=1+sin2x | D. | f(x)=ex+x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com