
| A. | ±$\sqrt{2}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{2}}{2}$ | D. | ±$\sqrt{3}$ |
分析 设AB的中点为M,过A、B、M分别作AA1、BB1、MN垂直于直线x=-1于A1、B1、N,设∠AFx=θ,求出sinθ=$\frac{1}{\sqrt{3}}$,即可求出直线AB的斜率.
解答 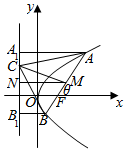 解:抛物线y2=4x的焦点为F(1,0),设AB的中点为M,过A、B、M分别作AA1、BB1、MN垂直于直线x=-1于A1、B1、N,设∠AFx=θ,
解:抛物线y2=4x的焦点为F(1,0),设AB的中点为M,过A、B、M分别作AA1、BB1、MN垂直于直线x=-1于A1、B1、N,设∠AFx=θ,
由抛物线定义知:|MN|=$\frac{1}{2}$(|AA1|+|BB1|)=$\frac{1}{2}$|AB|,
∵|MC|=$\frac{\sqrt{3}}{2}$|AB|,∴|MN|=$\frac{1}{\sqrt{3}}$|MC|,
∵∠CMN=90°-θ,
∴cos∠CMN=cos(90°-θ)=$\frac{|MN|}{|MC|}$=$\frac{1}{\sqrt{3}}$,即sinθ=$\frac{1}{\sqrt{3}}$,
∴tanθ=$\frac{\sqrt{2}}{2}$,
根据对称性,直线AB的斜率为±$\frac{\sqrt{2}}{2}$,
故选:C.
点评 本题考查抛物线的方程与性质,考查抛物线的定义,正确运用抛物线的定义是关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:选择题
| A. | k≥2 | B. | k≥4 | C. | 0<k≤2 | D. | 0<k≤4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,斜三棱柱ABC-A1B1C1中,平面ACC1A1⊥平面BCC1B1,E为棱CC1的中点,A1B与AB1交于点O.若AC=CC1=2BC=2,∠ACC1=∠CBB1=60°.
如图,斜三棱柱ABC-A1B1C1中,平面ACC1A1⊥平面BCC1B1,E为棱CC1的中点,A1B与AB1交于点O.若AC=CC1=2BC=2,∠ACC1=∠CBB1=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com