Question

关于x的不等式x²+25+|x³-5x²|≥ax在[1，12]上恒成立，则实数a的取值范围是________．

Answer 1

（-∞，10]
分析：分离参数a，把不等式变形为a≤x++|x²-5x|，只需a小于等于x++|x²-5x|的最小值即可．
解答：由x²+25+|x³-5x²|≥ax，1≤x≤12?a≤x++|x²-5x|，
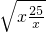
而x+≥2=10，当且仅当x=5∈[1，12]时取等号，
且|x²-5x|≥0，等号当且仅当x=5∈[1，12]时成立；
所以，a≤[x++|x2-5x|]min=10，等号当且仅当x=5∈[1，12]时成立；
故答案为：（-∞，10]；
点评：本题主要考查了函数恒成立问题以及绝对值不等式的解法、基本不等式在最值问题中的应用，本题中要注意等号须同时成立．