
已知函数f(x)=x3+ax2+bx+4(x∈R)在x=2处取得极小值.
(1)若函数f(x)的极小值是-4,求f(x);
(2)若函数f(x)的极小值不小于-6,问:是否存在实数k与函数f(x),使得函数f(x)在[k,k+3]上单调递减.若存在,求出k的取值集合与f(x);若不存在,说明理由.
科目:高中数学 来源: 题型:
函数f(x)=asin2x+bx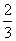 +4(a,b∈R),若f
+4(a,b∈R),若f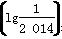 =2 013,则f(lg 2 014)=( )
=2 013,则f(lg 2 014)=( )
A.2 018 B.-2 009 C.2 013 D.-2 013
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等差数列{an}的前n项和为Sn,a4+a7+a10=9,S14-S3=77,则使Sn取得最小值时,n的值为( )
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=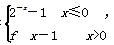 若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围为( )
若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围为( )
A.(-∞,0] B.[0,1)
C.(-∞,1) D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )
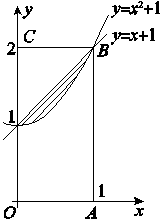
A.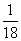 B.
B.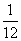 C.
C.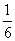 D.
D.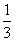
查看答案和解析>>
科目:高中数学 来源: 题型:
给出以下命题:
①双曲线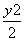 -x2=1的渐近线方程为y=±
-x2=1的渐近线方程为y=±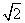 x;
x;
②命题p:“∀x∈R,sin x+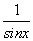 ≥2”是真命题;
≥2”是真命题;
③已知线性回归方程为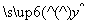 =3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
=3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
④设随机变量ξ服从正态分布N(0,σ2),若P(ξ>1)=0.2,则P(-1<ξ<0)=0.6;
⑤已知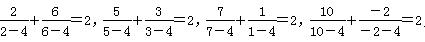 依照以上各式的规律,得到一般性的等式为
依照以上各式的规律,得到一般性的等式为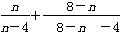 =2(n≠4).
=2(n≠4).
则正确命题的序号为________.(写出所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com