
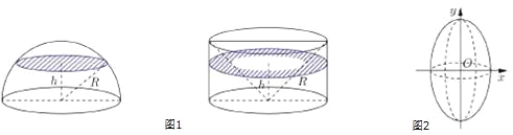
����Ŀ��(��ѧ�ľ���2017������ʮһ�и���12���¿���16��) �ֽ����敜ԭ�������������ʽ���������ɹ���һ������뾶�߶�����뾶��ȵ�Բ����Ȼ����Բ������ȥһ����Բ���µ���Բ��Ϊ���㣬Բ���ϵ���Ϊ�����Բ��������һ�������������Ӧ���敜ԭ����ͼ1�������������������ʽ�����о���������������ʽ�Ļ����ϣ�����������⣺��֪��Բ�ı�����Ϊ![]() ��������Բ��y����תһ�ܺ�һ���״�ļ����壨ͼ2�������������______��
��������Բ��y����תһ�ܺ�һ���״�ļ����壨ͼ2�������������______��
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��Բ
��Բ![]() ��Բ��
��Բ��![]() �����ҽ�����������
�����ҽ�����������![]() �Ľ����غ�.
�Ľ����غ�.
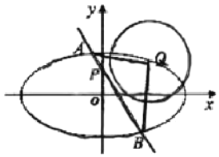
��1������Բ![]() �ķ���;
�ķ���;
��2������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ǽ�ͨ�¹ʶ�ڣ������Ż��˸�Σ���С���������Ƶ�����������˼��©����ũ�彻ͨ��æ���ĸ��������ս.ȫ���������ܲ���Ҫ�������ơ��������⣬��Խ����¹ʱ�¶���������⣬ǿ���𡢲��̰塢��©������һ���ƶ�����ж���������������ж��ɹ���ȫ��ȷ��������ͨ��ȫ�����ȶ�.�ݴˣ�ij��վ�Ƴ��˹��ڽ�ͨ��·��ȫ����ĵ��飬ͨ������������![]() ����Ⱥ�����ݱ�������ͨ��·��ȫ���ǰ�����Ϊ���ĵ��ȵ㣬����������й�ע���������Լռ80%.�ִӲ�����鲢��ע��ͨ��·��ȫ����Ⱥ�����ѡ��100�ˣ�������100�˰�������飺��1��
����Ⱥ�����ݱ�������ͨ��·��ȫ���ǰ�����Ϊ���ĵ��ȵ㣬����������й�ע���������Լռ80%.�ִӲ�����鲢��ע��ͨ��·��ȫ����Ⱥ�����ѡ��100�ˣ�������100�˰�������飺��1��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ����5��
����5��![]() ���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
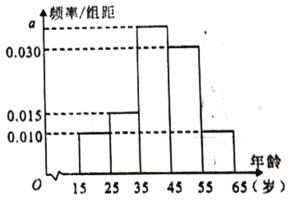
��1������100�����������ƽ������ͬһ�������ø�������е�ֵ������������λ������ȷ��С�����һλ����
��2������Ҫ������ϴ�ĵ�1��2�����÷ֲ�����ķ�����ȡ5�ˣ��ٴ���5���������ȡ2�˽����ʾ����飬���2��ǡ�ó鵽1�˵ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ����ȫ���������У��Ƴ������˴����ϵͳ������Ŀ��������Դ������Ϊ�����ع�.�������Ÿ���ijʮ��·�������ļ�����ݣ��Ӵ�Խ��·�ڵ���������������![]() �ˣ��õ���ͼʾ����������
�ˣ��õ���ͼʾ����������
����� | ������� | �ϼ� | |
���䲻���� |
|
|
|
���䳬�� |
|
|
|
�ϼ� |
|
|
|
��1���ܷ���![]() �İ�����Ϊ�������Ϊ�������йأ�
�İ�����Ϊ�������Ϊ�������йأ�
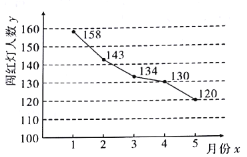
��2����ͼ��ij·�ڼ���豸ץ�ĵ�![]() �����������������ͳ��ͼ.�뽨��
�����������������ͳ��ͼ.�뽨��![]() ��
��![]() �Ļع鷽��
�Ļع鷽��![]() �������Ƹ�·��
�������Ƹ�·��![]() �·ݴ��������.
�·ݴ��������.
����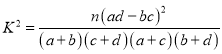
 ��
��![]()
|
|
|
|
|
|
|
|
|
|
|
|
�ο����ݣ�![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����![]() ����
����![]() ��
��![]() .
.
��1����![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ������
������![]() �����ϵʽ
�����ϵʽ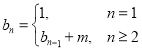 ����֤������
����֤������![]() ��ͨ�ʽΪ
��ͨ�ʽΪ![]() ��
��
��3���裨2���е�����![]() ��ǰn���Ϊ
��ǰn���Ϊ![]() ���������������n��
���������������n��![]() ���������ʵ��p��ȡֵ��Χ.
���������ʵ��p��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij֪��������![]() ˫ʮһ������гɽ����ٴ��¸ߣ�
˫ʮһ������гɽ����ٴ��¸ߣ�![]() ��
��![]() �յ��ճɽ����
�յ��ճɽ����![]() ��Ԫ.ij�����ڴ˴ι�����ڼ俪չ�˴������Ϊ�˽���ҶԴ˴δ��������������������ȡ�˲�����
��Ԫ.ij�����ڴ˴ι�����ڼ俪չ�˴������Ϊ�˽���ҶԴ˴δ��������������������ȡ�˲�����![]() λ��ң����������ǵ������κ�������������õ������ε�Ƶ�ʷֲ�ֱ��ͼ������������Ϊ��������������Ƶ���ֲ���.�����ε�Ƶ�ʷֲ�ֱ��ͼ��
λ��ң����������ǵ������κ�������������õ������ε�Ƶ�ʷֲ�ֱ��ͼ������������Ϊ��������������Ƶ���ֲ���.�����ε�Ƶ�ʷֲ�ֱ��ͼ��
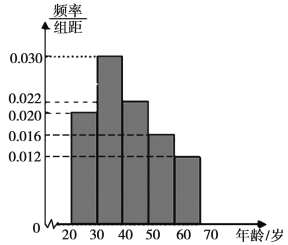
����������Ϊ���⡱��������Ƶ���ֲ�����
���䣨�꣩ |
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
��1�����Ʋ���˴λ����ҵ�ƽ�����䣨ͬһ���е������ø���������е�ֵ����������
��2����������![]() �����µij�Ϊ�������������������
�����µij�Ϊ�������������������![]() �����ϣ���
�����ϣ���![]() �꣩�ij�Ϊ��������������������������������ж��ܷ���
�꣩�ij�Ϊ��������������������������������ж��ܷ���![]() �İ�����Ϊ�С�������ҶԴ˴λ�������в��죿
�İ�����Ϊ�С�������ҶԴ˴λ�������в��죿
�������� | ���۲����� | �ϼ� | |
������� | |||
������� | |||
�ϼ� |
|
�����ο���ʽ��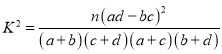 .
.
|
|
|
|
|
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() :
:![]() ��������Ϊ
��������Ϊ![]() ������Բ
������Բ![]() �ҽ���
�ҽ���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ���ڵ�
���ڵ�![]() ����
����![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���
����������Բ![]() �ķ��̣�
�ķ��̣�
��������֪![]() Ϊ��Բ
Ϊ��Բ![]() ���㣬ƽ����
���㣬ƽ����![]() ��ֱ��
��ֱ��![]() ����Բ�ཻ��
����Բ�ཻ��![]() ���㣮�ж�ֱ��
���㣮�ж�ֱ��![]() �Ƿ����ֱ��
�Ƿ����ֱ��![]() �Գƣ���˵�����ɣ�
�Գƣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�غ����еĺ������������ֱ��ֱ����·![]() ��
��![]() �������߽�
�������߽�![]() ���Ƶؿ���һ�����߶�.Ϊ����������Դ������һ������������·��ֱ���۹���
���Ƶؿ���һ�����߶�.Ϊ����������Դ������һ������������·��ֱ���۹���![]() ����ֱ��
����ֱ��![]() ������
������![]() ���ҽ���һ��������P����ֱ�����������У�����ͼ��ʾ�������߶�
���ҽ���һ��������P����ֱ�����������У�����ͼ��ʾ�������߶�![]() �Ǻ���
�Ǻ���![]() ͼ���һ�Σ���M��
ͼ���һ�Σ���M��![]() ��
��![]() �ľ���ֱ�Ϊ8ǧ��1ǧ�ף���N��
�ľ���ֱ�Ϊ8ǧ��1ǧ�ף���N��![]() �ľ���Ϊ10ǧ�ף���P��
�ľ���Ϊ10ǧ�ף���P��![]() �ľ���Ϊ2ǧ��.��
�ľ���Ϊ2ǧ��.��![]() ��
��![]() �ֱ�Ϊx��y�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵ
�ֱ�Ϊx��y�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵ![]() .
.
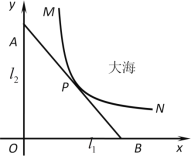
��1�������߶�![]() �ĺ�����ϵʽ����ָ���䶨����
�ĺ�����ϵʽ����ָ���䶨����
��2����ֱ��![]() �ķ��̣��������·
�ķ��̣��������·![]() �ij��ȣ������ȷ��1�ף�.
�ij��ȣ������ȷ��1�ף�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �������Σ�
�������Σ� ![]() ƽ��
ƽ��![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ���е�.
���е�.
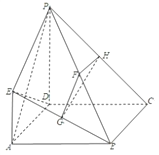
��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵĴ�С��
���������ǵĴ�С��
��3�����߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹֱ��
��ʹֱ��![]() ��ֱ��
��ֱ��![]() ���ɵĽ�Ϊ
���ɵĽ�Ϊ![]() �������ڣ�����߶�
�������ڣ�����߶�![]() �ij����������ڣ���˵������.
�ij����������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com