
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(1)![]() ;(2)第一种方案;(3)详见解析
;(2)第一种方案;(3)详见解析
【解析】
(1)计算出从![]() 个水果中随机抽取一个,抽到礼品果的概率;则可利用二项分布的概率公式求得所求概率;(2)计算出方案
个水果中随机抽取一个,抽到礼品果的概率;则可利用二项分布的概率公式求得所求概率;(2)计算出方案![]() 单价的数学期望,与方案
单价的数学期望,与方案![]() 的单价比较,选择单价较低的方案;(3)根据分层抽样原则确定抽取的
的单价比较,选择单价较低的方案;(3)根据分层抽样原则确定抽取的![]() 个水果中,精品果
个水果中,精品果![]() 个,非精品果
个,非精品果![]() 个;则
个;则![]() 服从超几何分布,利用超几何分布的概率计算公式可得到每个
服从超几何分布,利用超几何分布的概率计算公式可得到每个![]() 取值对应的概率,从而可得分布列;再利用数学期望的计算公式求得结果.
取值对应的概率,从而可得分布列;再利用数学期望的计算公式求得结果.
(1)设从![]() 个水果中随机抽取一个,抽到礼品果的事件为
个水果中随机抽取一个,抽到礼品果的事件为![]() ,则
,则![]()
现有放回地随机抽取![]() 个,设抽到礼品果的个数为
个,设抽到礼品果的个数为![]() ,则
,则![]()
![]() 恰好抽到
恰好抽到![]() 个礼品果的概率为:
个礼品果的概率为:![]()
(2)设方案![]() 的单价为
的单价为![]() ,则单价的期望值为:
,则单价的期望值为:
![]()
![]()
![]() 从采购商的角度考虑,应该采用第一种方案
从采购商的角度考虑,应该采用第一种方案
(3)用分层抽样的方法从![]() 个水果中抽取
个水果中抽取![]() 个,则其中精品果
个,则其中精品果![]() 个,非精品果
个,非精品果![]() 个
个
现从中抽取![]() 个,则精品果的数量
个,则精品果的数量![]() 服从超几何分布,所有可能的取值为:
服从超几何分布,所有可能的取值为:![]()
则![]() ;
;![]() ;
;![]() ;
;![]()
![]() 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
|
|
![]()


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】2015年“双十一”当天,甲、乙两大电商进行了打折促销活动,某公司分别调查了当天在甲、乙电商购物的1000名消费者的消费金额,得到了消费金额的频数分布表如下:
甲电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 50 | 200 | 350 | 300 | 100 |
乙电商:
消费金额(单位:千元) | [0,1) | [1,2) | [2,3) | [3,4) | [4,5] |
频数 | 250 | 300 | 150 | 100 | 200 |
(Ⅰ)根据频数分布表,完成下列频率分布直方图,并根据频率分布直方图比较消费者在甲、乙电商消费金额的中位数的大小以及方差的大小(其中方差大小给出判断即可,不必说明理由);
(Ⅱ)(ⅰ)根据上述数据,估计“双十一”当天在甲电商购物的大量的消费者中,消费金额小于3千元的概率;
(ⅱ)现从“双十一”当天在甲电商购物的大量的消费者中任意调查5位,记消费金额小于3千元的人数为X,试求出X的期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率
的离心率![]() ,且圆
,且圆![]() 经过椭圆C的上、下顶点.
经过椭圆C的上、下顶点.
(1)求椭圆C的方程;
(2)若直线l与椭圆C相切,且与椭圆![]() 相交于M,N两点,证明:
相交于M,N两点,证明:![]() 的面积为定值(O为坐标原点).
的面积为定值(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() (常数
(常数![]() )相交于不同的两点
)相交于不同的两点![]() 、
、![]() ,且
,且![]() (
(![]() 为定值),线段
为定值),线段![]() 的中点为
的中点为![]() ,与直线
,与直线![]() 平行的切线的切点为
平行的切线的切点为![]() (不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).

(1)用![]() 、
、![]() 表示出
表示出![]() 点、
点、![]() 点的坐标,并证明
点的坐标,并证明![]() 垂直于
垂直于![]() 轴;
轴;
(2)求![]() 的面积,证明
的面积,证明![]() 的面积与
的面积与![]() 、
、![]() 无关,只与
无关,只与![]() 有关;
有关;
(3)小张所在的兴趣小组完成上面两个小题后,小张连![]() 、
、![]() ,再作与
,再作与![]() 、
、![]() 平行的切线,切点分别为
平行的切线,切点分别为![]() 、
、![]() ,小张马上写出了
,小张马上写出了![]() 、
、![]() 的面积,由此小张求出了直线
的面积,由此小张求出了直线![]() 与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
与抛物线围成的面积,你认为小张能做到吗?请你说出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校艺术专业300名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
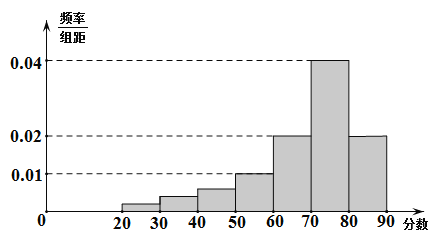
(1)从总体的300名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px的焦点为F,准线方程是x=﹣1.
(I)求此抛物线的方程;
(Ⅱ)设点M在此抛物线上,且|MF|=3,若O为坐标原点,求△OFM的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题
(1)若一条直线与两条直线都相交,那么这三条直线共面;
(2)若三条直线两两平行,那么这三条直线共面;
(3)若直线![]() 与直线
与直线![]() 异面,直线
异面,直线![]() 与直线
与直线![]() 异面,那么直线
异面,那么直线![]() 与直线
与直线![]() 异面;
异面;
(4)若直线![]() 与直线
与直线![]() 垂直,直线
垂直,直线![]() 与直线
与直线![]() 垂直,那么直线
垂直,那么直线![]() 与直线
与直线![]() 平行;
平行;
其中正确的命题个数有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,与
,与![]() 轴正半轴交于两点
轴正半轴交于两点![]() ,
,![]() (
(![]() 在
在![]() 的上方),且
的上方),且![]() .
.
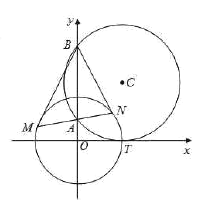
(1)求圆![]() 的标准方程;
的标准方程;
(2)过点![]() 作任一条直线与圆
作任一条直线与圆![]() :
:![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
①求证:![]() 为定值,并求出这个定值;
为定值,并求出这个定值;
②求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com