
分析 (1)把点A($\sqrt{2}$,$\frac{π}{4}$)代入直线l的极坐标方程ρcos(θ-$\frac{π}{4}$)=a,可得a=$\sqrt{2}$.展开$ρ×\frac{\sqrt{2}}{2}(cosθ+sinθ)$=$\sqrt{2}$,利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出.曲线C的极坐标方程为ρ2=$\frac{12}{3+si{n}^{2}θ}$,化为3ρ2+(ρsinθ)2=12,代入$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$即可得出.联立解出即可得出点P,Q两点的坐标.
(II)直线l1的参数方程为:$\left\{\begin{array}{l}{x=-2-\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),代入曲线C的方程利用|BM|•|BN|=t1t2即可得出.
解答 解:(1)把点A($\sqrt{2}$,$\frac{π}{4}$)代入直线l的极坐标方程ρcos(θ-$\frac{π}{4}$)=a,可得$\sqrt{2}cos0$=a,解得a=$\sqrt{2}$.
∴$ρ×\frac{\sqrt{2}}{2}(cosθ+sinθ)$=$\sqrt{2}$,化为直角坐标方程x+y-2=0.
曲线C的极坐标方程为ρ2=$\frac{12}{3+si{n}^{2}θ}$,化为3ρ2+(ρsinθ)2=12,
∴直角坐标方程为3x2+4y2=12,化为标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
联立$\left\{\begin{array}{l}{x+y-2=0}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,化为7y2-12y=0,解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{2}{7}}\\{y=\frac{12}{7}}\end{array}\right.$.
∴P(2,0),Q$(\frac{2}{7},\frac{12}{7})$.
(II)直线l1的参数方程为:$\left\{\begin{array}{l}{x=-2-\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),代入曲线C的方程为:$7{t}^{2}+28\sqrt{2}t+32$=0,
∴t1t2=$\frac{32}{7}$.
∴|BM|•|BN|=t1t2=$\frac{32}{7}$.
点评 本题考查了极坐标化为直角坐标方程的方法、直线与椭圆相交交点问题、直线的参数方程应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ±1 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | -2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
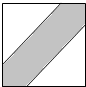 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )| A. | $\frac{529}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{23}{25}$ | D. | $\frac{2}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<1 | B. | 0≤a≤1 | C. | 0<a≤1 | D. | 0≤a<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com