分析：（I）直线l∥平面PAC．连接EF，利用三角形的中位线定理可得，EF∥AC；利用线面平行的判定定理即可得到EF∥平面ABC．由线面平行的性质定理可得EF∥l．再利用线面平行的判定定理即可证明直线l∥平面PAC．
（II）综合法：利用线面垂直的判定定理可证明l⊥平面PBC．连接BE，BF，因为BF?平面PBC，所以l⊥BC．故∠CBF就是二面角E-l-C的平面角，即∠CBF=β．
已知PC⊥平面ABC，可知CD是FD在平面ABC内的射影，故∠CDF就是直线PQ与平面ABC所成的角，即∠CDF=θ．由BD⊥平面PBC，有BD⊥BF，知∠BDF=α，分别利用三个直角三角形的边角关系即可证明结论；
向量法：以点C为原点，向量
，，所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系，利用两个平面的法向量的夹角即可得出二面角．
解答：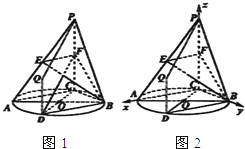
解：（Ⅰ）直线l∥平面PAC，证明如下：
连接EF，因为E，F分别是PA，PC的中点，所以EF∥AC，
又EF?平面ABC，且AC?平面ABC，所以EF∥平面ABC．
而EF?平面BEF，且平面BEF∩平面ABC=l，所以EF∥l．
因为l?平面PAC，EF?平面PAC，所以直线l∥平面PAC．
（Ⅱ）（综合法）如图1，连接BD，由（Ⅰ）可知交线l即为直线BD，且l∥AC．
因为AB是⊙O的直径，所以AC⊥BC，于是l⊥BC．
已知PC⊥平面ABC，而l?平面ABC，所以PC⊥l．
而PC∩BC=C，所以l⊥平面PBC．
连接BE，BF，因为BF?平面PBC，所以l⊥BF．
故∠CBF就是二面角E-l-C的平面角，即∠CBF=β．
由
=，作DQ∥CP，且
DQ=CP．
连接PQ，DF，因为F是CP的中点，CP=2PF，所以DQ=PF，
从而四边形DQPF是平行四边形，PQ∥FD．
连接CD，因为PC⊥平面ABC，所以CD是FD在平面ABC内的射影，
故∠CDF就是直线PQ与平面ABC所成的角，即∠CDF=θ．
又BD⊥平面PBC，有BD⊥BF，知∠BDF=α，
于是在Rt△DCF，Rt△FBD，Rt△BCF中，分别可得
sinθ=，sinα=，sinβ=，
从而
sinαsinβ=•==sinθ，即sinθ=sinαsinβ．
（Ⅱ）（向量法）如图2，由
=，作DQ∥CP，且
DQ=CP．
连接PQ，EF，BE，BF，BD，由（Ⅰ）可知交线l即为直线BD．
以点C为原点，向量
，，所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系，设CA=a，CB=b，CP=2c，则有
C(0，0，0)，A(a，0，0)，B(0，b，0)，P(0，0，2c)，Q(a，b，c)，E(a，0，c)，F(0，0，c)．
于是
=(a，0，0)，=(-a，-b，c)，=(0，-b，c)，
∴
cosα==
，从而
sinα==，
又取平面ABC的一个法向量为
=(0，0，1)，可得
sinθ==，
设平面BEF的一个法向量为
=(x，y，z)，
所以由
可得
取(0，c，b)．
于是
|cosβ|==，从而
sinβ==．
故
sinαsinβ=•==sinθ，即sinθ=sinαsinβ．
（2013•湖北）如图，AB是圆O的直径，点C是圆O上异于A，B的点，直线PC⊥平面ABC，E，F分别是PA，PC的中点．
（2013•湖北）如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X，则X的均值E（X）=（ ）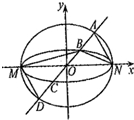
（2013•湖北）如图，已知椭圆C1与C2的中心在坐标原点O，长轴均为MN且在x轴上，短轴长分别为2m，2n（m＞n），过原点且不与x轴重合的直线l与C1，C2的四个交点按纵坐标从大到小依次为A，B，C，D，记λ=
（2013•湖北）如图，某地质队自水平地面A，B，C三处垂直向地下钻探，自A点向下钻到A1处发现矿藏，再继续下钻到A2处后下面已无矿，从而得到在A处正下方的矿层厚度为A1A2=d1．同样可得在B，C处正下方的矿层厚度分别为B1B2=d2，C1C2=d3，且d1＜d2＜d3．过AB，AC的中点M，N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面，其面积记为S中．