
| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用向量垂直的条件,结合向量数量积公式,即可求向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角
解答 解:设向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,
∵|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{a}$=${\overline{a}}^{2}$+$\overrightarrow{a}•\overrightarrow{b}$=${\overline{a}}^{2}$+|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=2+2$\sqrt{2}$cosθ=0,
解得cosθ=-$\frac{\sqrt{2}}{2}$,
∵0≤θ≤π,
∴θ=$\frac{3π}{4}$,
故选:A
点评 本题考查向量的夹角的计算,考查向量数量积公式的运用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
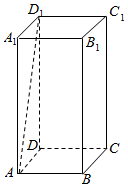 如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2BC=2,则异面直线A1B与AD1所成角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,AA1=2AB=2BC=2,则异面直线A1B与AD1所成角的余弦值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
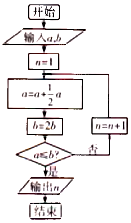 《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )
《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
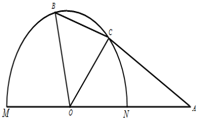 如图,半径为1的半圆O上有一动点B,MN为直径,A为半径ON延长线上的一点,且OA=2,∠AOB的角平分线交半圆于点C.
如图,半径为1的半圆O上有一动点B,MN为直径,A为半径ON延长线上的一点,且OA=2,∠AOB的角平分线交半圆于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com