
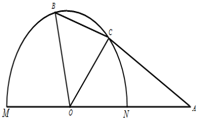
 如图,半径为1的半圆O上有一动点B,MN为直径,A为半径ON延长线上的一点,且OA=2,∠AOB的角平分线交半圆于点C.
如图,半径为1的半圆O上有一动点B,MN为直径,A为半径ON延长线上的一点,且OA=2,∠AOB的角平分线交半圆于点C.分析 (1)若$\overrightarrow{AC}•\overrightarrow{AB}=3$,利用向量的数量积公式,即可求cos∠AOC的值;
(2)若A,B,C三点共线,可得$cosθ=\frac{3}{4}$,利用余弦定理,即可求线段AC的长.
解答 解:(1)设∠AOC=θ,$\overrightarrow{AC}=\overrightarrow{AO}+\overrightarrow{OC}$,$\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}$(2分)∴$\overrightarrow{AC}•\overrightarrow{AB}=({\overrightarrow{AO}+\overrightarrow{OC}})•({\overrightarrow{AO}+\overrightarrow{OB}})={\overrightarrow{AO}^2}+\overrightarrow{AO}•\overrightarrow{OB}+\overrightarrow{OC}•\overrightarrow{AO}+\overrightarrow{OC}•\overrightarrow{OB}$
=4+1×2×cos(π-2θ)+1×2×cos(π-θ)+cosθ
=-4cos2θ-cosθ+6(2分)
∴-4cos2θ-cosθ+6=3,∴$cosθ=\frac{3}{4},cosθ=-1$(舍去)(3分)
(2)A,B,C三点共线,
所以$\frac{cos2θ-2}{cosθ-2}=\frac{sin2θ}{sinθ}$(2分)∴$cosθ=\frac{3}{4}$(1分)
∴AC2=1+4-2×1×2×cosθ=2,∴$|{AC}|=\sqrt{2}$(2分).
点评 本题考查向量的运算,考查余弦定理的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
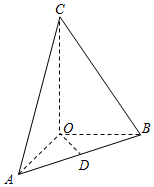 在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.
在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com