
【题目】设A(n)表示正整数n的个位数,an=A(n2)﹣A(n),A为数列{an}的前202项和,函数f(x)=ex﹣e+1,若函数g(x)满足f[g(x)﹣ ![]() ]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
]=1,且bn=g(n)(n∈N*),则数列{bn}的前n项和为 .
【答案】n+3﹣(2n+3)?( ![]() )n
)n
【解析】解:n的个位数为1时有:an=A(n2)﹣A(n)=0,
n的个位数为2时有:an=A(n2)﹣A(n)=4﹣2=2,
n的个位数为3时有:an=A(n2)﹣A(n)=9﹣3=6,
n的个位数为4时有:an=A(n2)﹣A(n)=6﹣4=2,
n的个位数为5时有:an=A(n2)﹣A(n)=5﹣5=0,
n的个位数为6时有:an=A(n2)﹣A(n)=6﹣6=0,
n的个位数为7时有:an=A(n2)﹣A(n)=9﹣7=2,
n的个位数为8时有:an=A(n2)﹣A(n)=4﹣8=﹣4,
n的个位数为9时有:an=A(n2)﹣A(n)=1﹣9=﹣8,
n的个位数为0时有:an=A(n2)﹣A(n)=0﹣0=0,
每10个一循环,这10个数的和为:0,
202÷10=20余2,余下两个数为:a201=0,a202=2,
∴数列{an}的前202项和等于:a201+a202=0+2=2,
即有A=2.
函数函数f(x)=ex﹣e+1为R上的增函数,且f(1)=1,
f[g(x)﹣ ![]() ]=1=f(1),
]=1=f(1),
可得g(x)=1+ ![]() =1+
=1+ ![]() ,
,
则g(n)=1+(2n﹣1)( ![]() )n,
)n,
即有bn=g(n)=1+(2n﹣1)( ![]() )n,
)n,
则数列{bn}的前n项和为n+[1( ![]() )1+3(
)1+3( ![]() )2+5(
)2+5( ![]() )3++(2n﹣1)(
)3++(2n﹣1)( ![]() )n],
)n],
可令S=1( ![]() )1+3(
)1+3( ![]() )2+5(
)2+5( ![]() )3++(2n﹣1)(
)3++(2n﹣1)( ![]() )n,
)n,
![]() S=1(
S=1( ![]() )2+3(
)2+3( ![]() )3+5(
)3+5( ![]() )4++(2n﹣1)(
)4++(2n﹣1)( ![]() )n+1,
)n+1,
两式相减可得 ![]() S=
S= ![]() +2[(
+2[( ![]() )2+(
)2+( ![]() )3+(
)3+( ![]() )4++(
)4++( ![]() )n]﹣(2n﹣1)(
)n]﹣(2n﹣1)( ![]() )n+1
)n+1
= ![]() +2
+2 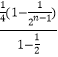 ﹣(2n﹣1)(
﹣(2n﹣1)( ![]() )n+1,
)n+1,
化简可得S=3﹣(2n+3)( ![]() )n,
)n,
则数列{bn}的前n项和为n+3﹣(2n+3)( ![]() )n.
)n.
故答案为:n+3﹣(2n+3)( ![]() )n.
)n.
先根据n的个位数的不同取值推导数列的周期,由周期可求得A=2,再由函数f(x)为R上的增函数,求得g(x)的解析式,即有bn=g(n)=1+(2n﹣1)( ![]() )n,再由数列的求和方法:分组求和和错位相减法,化简整理即可得到所求和.
)n,再由数列的求和方法:分组求和和错位相减法,化简整理即可得到所求和.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,PA⊥平面ABC,△ABC为正三角形,PA=AB,E是PC的中点,则异面直线AE和PB所成角的余弦值为( ) 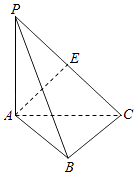
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题P:函数f(x)=log2m(x+1)是增函数;命题Q:x∈R,x2+mx+1≥0.
(1)写出命题Q的否命题¬Q;并求出实数m的取值范围,使得命题¬Q为真命题;
(2)如果“P∨Q”为真命题,“P∧Q”为假命题,求实数m的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.

(1)求证:OE∥平面BCC1B1.
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对直线不互相垂直的是 ( )
A. l1的倾斜角为120°,l2过点P(1,0),Q(4, ![]() )
)
B. l1的斜率为-![]() ,l2过点P(1,1),Q
,l2过点P(1,1),Q![]()
C. l1的倾斜角为30°,l2过点P(3, ![]() ),Q(4,2
),Q(4,2![]() )
)
D. l1过点M(1,0),N(4,-5),l2过点P(-6,0),Q(-1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 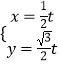 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2 ![]() ,
, ![]() ). (Ⅰ)求直线l以及曲线C的极坐标方程;
). (Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线a,b和平面M,N,且a⊥M,则下列说法正确的是 ( )
A. b∥Mb⊥a B. b⊥ab∥M
C. N⊥Ma∥N D. aNM∩N≠
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2﹣2lnx,x∈(0,e],其中e是自然对数的底.
(1)若f(x)在x=1处取得极值,求a的值;
(2)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若在区间[0,1]上有最大值1和最小值-2.求a,b的值;
(2)在(1)条件下,若在区间![]() 上,不等式f(x)
上,不等式f(x)![]()
![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com