
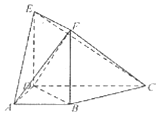
 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,分析 (1)以D为原点,DA、DC‘DE为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能证明CE⊥DF.
(2)求出平面EFC的一个法向量,利用向量法推导出在棱AE上存在点G,使得直线BG∥平面EFC,且$\frac{AG}{GE}$=$\frac{1}{2}$.
解答 证明:(1)∵梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,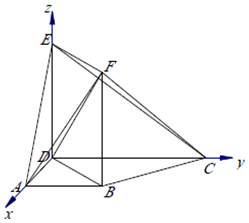
平面BDEF丄平面ABCD,BD⊥CF,AF⊥CE,
∴DA、DC、DE两两垂直,
∴以D为原点,DA、DC‘DE为x轴,y轴,z轴,建立空间直角坐标系,
设DE=m,AB=y,则D(0,0,0),B(1,y,0),A(1,0,0),E(0,0,m),F(1,y,m),C(0,2,0),
$\overrightarrow{DB}=(1,y,0),\overrightarrow{CF}=(1,y-2,m)$,
∵BD⊥CF,∴$\overrightarrow{DB}•\overrightarrow{CF}=1+{y}^{2}-2y=0$,解得y=1,
∴$\overrightarrow{AF}$=(0,1,m),$\overrightarrow{CE}$=(0,-2,m),$\overrightarrow{DF}$=(1,1,m),
∵AF⊥CE,∴$\overrightarrow{AF}•\overrightarrow{CE}$=-2+m2=0,
∵$\overrightarrow{CE}•\overrightarrow{DF}$=-2+m2,∴$\overrightarrow{CE}•\overrightarrow{DF}$=0,
∴CE⊥DF.
解:(2)在棱AE上存在点G,使得直线BG∥平面EFC,且$\frac{AG}{GE}$=$\frac{1}{2}$.
证明如下:
由(1)知G($\frac{2}{3},0,\frac{m}{3}$),
∴$\overrightarrow{BG}$=(-$\frac{1}{3},-1,\frac{m}{3}$),$\overrightarrow{EF}$=(1,1,0),$\overrightarrow{EC}$=(0,2,-m),
设平面EFC的一个法向量$\overrightarrow{n}$=(a,b,c),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EF}=a+b=0}\\{\overrightarrow{n}•\overrightarrow{EC}=2b-mc=0}\end{array}\right.$,取b=1,得$\overrightarrow{n}$=(-1,1,$\frac{2}{m}$),
∵$\overrightarrow{BG}•\overrightarrow{n}$=(-$\frac{1}{3}$)×(-1)+(-1)×1+$\frac{m}{3}•\frac{2}{m}$=0,
∴$\overrightarrow{BG}⊥\overrightarrow{n}$,
∵BG?平面EFC,
∴BG∥平面EFC.
点评 本题考查线线垂直的证明,考查满足线面平行的点是否存在的判断与求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、数据处理能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| f(x) | 2 | 0 | 3 | 1 |
| x | 0 | 1 | 2 | 3 |
| g(x) | 2 | 1 | 0 | 3 |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2+1(x≠0) | B. | y=x2+3(x≠0) | ||
| C. | y2-$\frac{{x}^{2}}{2}$=1(y>0,x≠0) | D. | y=3(x≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | -1+i | C. | 1-i | D. | -1-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
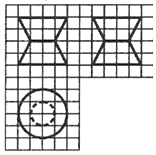 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com