
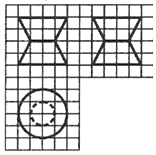
 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
分析 由已知中的三视图,可知该几何体是一个圆柱切削得到,是两个圆台对接可得.计算其中一个圆台的体积和计算圆柱的体积可得,削切削掉部分的体积与原毛坯体积的比值.
解答 解:由题意,把该几何体看出是两个圆台对接可得,圆台上下半径分别为1,2,高为2,
∴一个圆台的体积为:V1=$\frac{1}{3}$πh(r2+r′r+r′2)=$\frac{1}{3}$×2×7π=$\frac{14}{3}$$\frac{π}{\;}$,
该几何体的体积为:V=2V1=$\frac{28}{3}$π;
圆柱的体积为:V=Sh=π×22×4=16π.
削切削掉部分的体积为:16π-$\frac{28π}{3}$=$\frac{20π}{3}$,
削切削掉部分的体积与原毛坯体积的比值:即$\frac{20π}{3}$:16π=$\frac{5}{12}$.
故选C
点评 本题考查的知识点是圆柱,圆台的三视图体积求法,解决本题的关键是得到该几何体的形状.


科目:高中数学 来源: 题型:选择题
| A. | i | B. | 2i | C. | 3i | D. | 5i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
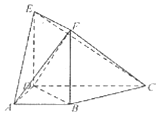 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | C-1 | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com