
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
分析 先求出基本事件总数n=${C}_{5}^{2}=10$,再求出所取出的2个球颜色不同包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,由此能求出所取出的2个球颜色不同的概率.
解答 解:盒中装有形状,大小完全相同的5个小球,其中红色球3个,黄色球2个,
从中随机取出2个球,
基本事件总数n=${C}_{5}^{2}=10$,
所取出的2个球颜色不同包含的基本事件个数m=${C}_{2}^{1}{C}_{3}^{1}$=6,
所取出的2个球颜色不同的概率等于p=$\frac{m}{n}$=$\frac{6}{10}=\frac{3}{5}$.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x2+1(x≠0) | B. | y=x2+3(x≠0) | ||
| C. | y2-$\frac{{x}^{2}}{2}$=1(y>0,x≠0) | D. | y=3(x≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
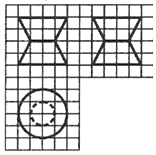 如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )
如图,网格纸上小正方形的边长为1,图中粗线画出的是某零件的三视图,该零件由一个底曲直径为4,高为4的圆柱体毛坯切削得到,削切削掉部分的体积与原毛坯体积的比值为( )| A. | $\frac{3}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{5}{12}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
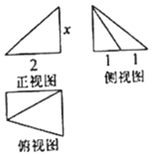
| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
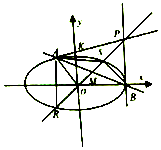 中心在原点,焦点在x轴上的椭圆C过点K(0,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,点M($\frac{2}{3}$,$\frac{2}{3}$)在椭圆C内,椭圆C上两点A,B满足$\overrightarrow{AM}$=$\overrightarrow{MB}$.
中心在原点,焦点在x轴上的椭圆C过点K(0,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,点M($\frac{2}{3}$,$\frac{2}{3}$)在椭圆C内,椭圆C上两点A,B满足$\overrightarrow{AM}$=$\overrightarrow{MB}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com