
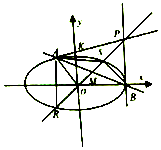
 中心在原点,焦点在x轴上的椭圆C过点K(0,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,点M($\frac{2}{3}$,$\frac{2}{3}$)在椭圆C内,椭圆C上两点A,B满足$\overrightarrow{AM}$=$\overrightarrow{MB}$.
中心在原点,焦点在x轴上的椭圆C过点K(0,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,点M($\frac{2}{3}$,$\frac{2}{3}$)在椭圆C内,椭圆C上两点A,B满足$\overrightarrow{AM}$=$\overrightarrow{MB}$.分析 (1)由题意,b=$\sqrt{2}$,e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$,求出a,b可得椭圆C的方程;
(2)利用点差法,即可求直线AB的斜率;
(3)求出P的坐标,证明kOM=kOP=1,即可证明O,M,P三点共线;要证S△AOR•S△BOS=S△AOM•S△BOP,只要证|OR|•|OS|=|OM|•|OP|.
解答 (1)解:由题意,b=$\sqrt{2}$,又e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$,得$\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$,
得a2=2b2=4,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)解:设A(x1,y1),B(x2,y2),由$\overrightarrow{AM}$=$\overrightarrow{MB}$,知M为A,B的中点,
由$\frac{{{x}_{1}}^{2}}{4}+\frac{{{y}_{1}}^{2}}{2}=1$,$\frac{{{x}_{2}}^{2}}{4}+\frac{{{y}_{2}}^{2}}{2}=1$,两式作差可得:$\frac{({x}_{1}-{x}_{2})({x}_{1}+{x}_{2})}{4}=-\frac{({y}_{1}-{y}_{2})({y}_{1}+{y}_{2})}{2}$,
∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}=-\frac{2({x}_{1}+{x}_{2})}{4({y}_{1}+{y}_{2})}$=$-\frac{1}{2}$,
∴直线AB的斜率k=$-\frac{1}{2}$;
(3)证明:直线AB的方程为y=-$\frac{1}{2}$x+1,∴B(2,0),A(-$\frac{2}{3}$,$\frac{4}{3}$),
过B的切线方程为x=2,
由$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$,可得y=$\sqrt{2-\frac{{x}^{2}}{2}}$,y′=-$\frac{x}{2\sqrt{2-\frac{{x}^{2}}{2}}}$,x=-$\frac{2}{3}$,y′=$\frac{1}{4}$,
∴过A的切线方程为y-$\frac{4}{3}$=$\frac{1}{4}$(x+$\frac{2}{3}$),即y=$\frac{1}{4}$x+$\frac{3}{2}$,
x=2时,y=2,即P(2,2).∴kOP=1
∵M($\frac{2}{3}$,$\frac{2}{3}$),∴kOM=1,
∴kOM=kOP=1,
∴O,M,P三点共线.
要证S△AOR•S△BOS=S△AOM•S△BOP,只要证|OR|•|OS|=|OM|•|OP|.
直线OM的方程y=x与椭圆方程联立可得R(-$\frac{2\sqrt{3}}{3}$,-$\frac{2\sqrt{3}}{3}$),S($\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$),∴|OR|•|OS|=|$\frac{8}{3}$,
∵|OM|•|OP|=$\frac{2\sqrt{2}}{3}•2\sqrt{2}$=$\frac{8}{3}$,
∴|OR|•|OS|=|OM|•|OP|,
∴S△AOR•S△BOS=S△AOM•S△BOP.
点评 本题考查了椭圆方程,考查点差法的运用,考查学生分析解决问题的能力,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}}}{9}$ | B. | $-\frac{{2\sqrt{2}}}{9}$ | C. | $\frac{1}{9}$ | D. | $-\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{4}$ | B. | $\frac{π}{2}$-1 | C. | $\frac{π-1}{4}$ | D. | $\frac{π-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com