
分析 (1)设点P(x',y'),点M的坐标为(x,y),由题意可知x′=x,y′=2y,由此能求出点M的轨迹C的方程,进一步求出椭圆的离心率;
(2)四边形ABF1F2面积S,S=S△ABO+${S}_{△B{F}_{1}O}$+${S}_{△A{F}_{2}O}$,设直线AB:y=kx+m,代入椭圆方程,利用点到直线的距离公式及丨AB丨=2$\sqrt{4-\frac{{m}^{2}}{{k}^{2}+1}}$,求得S△ABO,将直线方程代入圆的方程,利用韦达定理,求得${S}_{△B{F}_{1}O}$+${S}_{△A{F}_{2}O}$,由k2=$\frac{{m}^{2}-1}{4}$,易知k2≥0,求得丨m丨≥1,利用基本不等式的性质,即可求得四边形ABF1F2面积的最大值.
解答 解:(1)设圆O上点P(x',y'),曲线C上点M的坐标为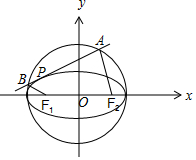
由题意可知x′=x,y′=2y,
又x'2+y'2=4,∴x2+4y2=4,即$\frac{{x}^{2}}{4}+{y}^{2}$=1.
∴点M的轨迹C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1,则a2=4,b2=1,
$c=\sqrt{{a}^{2}-{b}^{2}}=\sqrt{3}$,
离心率e=$\frac{\sqrt{3}}{2}$;
(2)易知直线AB的斜率k存在,设AB:y=kx+m,A(x1,y1),B(x2,y2),
则$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,(4k2+1)x2+8kmx+4(m2-1)=0,
则△=(8km)2-16(4k2+1)(m2-1)=0,整理得:4k2-m2+1=0,即m2=4k2+1,
由四边形ABF1F2面积S,S=S△ABO+${S}_{△B{F}_{1}O}$+${S}_{△A{F}_{2}O}$,
设点O到直线AB:kx-y+m=0的距离为d,d=$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$,
则丨AB丨=2$\sqrt{丨OA{丨}^{2}-{d}^{2}}$=2$\sqrt{4-\frac{{m}^{2}}{{k}^{2}+1}}$,
S△ABO=$\frac{1}{2}$×2$\sqrt{4-\frac{{m}^{2}}{{k}^{2}+1}}$×$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$,
=$\sqrt{4-\frac{{m}^{2}}{{k}^{2}+1}}$×$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$,
=$\frac{\sqrt{(4{k}^{2}+4-{m}^{2}){m}^{2}}}{{k}^{2}+1}$=$\frac{\sqrt{3}丨m丨}{{k}^{2}+1}$,
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+{y}^{2}=4}\end{array}\right.$,整理得:(k2+1)x2+2kmx+m2-4=0,
由韦达定理可知:x1+x2=-$\frac{2km}{{k}^{2}+1}$,x1x2=$\frac{{m}^{2}-4}{{k}^{2}+1}$,
y1+y1=kx1+m+kx2+m=k(x1+x2)+2m=$\frac{2m}{{k}^{2}+1}$,
${S}_{△B{F}_{1}O}$+${S}_{△A{F}_{2}O}$=$\frac{1}{2}$×$\sqrt{3}$丨y1丨+$\frac{1}{2}$×$\sqrt{3}$丨y2丨=$\frac{\sqrt{3}}{2}$(丨y1丨+丨y2丨)=$\frac{\sqrt{3}}{2}$丨y1+y2丨=$\frac{\sqrt{3}丨m丨}{{k}^{2}+1}$,
S=S△ABO+(${S}_{△B{F}_{1}O}$+${S}_{△A{F}_{2}O}$)=$\frac{\sqrt{3}丨m丨}{{k}^{2}+1}$+$\frac{\sqrt{3}丨m丨}{{k}^{2}+1}$=$\frac{2\sqrt{3}丨m丨}{{k}^{2}+1}$
而m2=4k2+1,k2=$\frac{{m}^{2}-1}{4}$,易知k2≥0,
∴m2≥1,丨m丨≥1,
四边形ABF1F2面积S,S=$\frac{2\sqrt{3}丨m丨}{\frac{{m}^{2}-1}{4}+1}$=$\frac{8\sqrt{3}丨m丨}{{m}^{2}+3}$=$\frac{8\sqrt{3}}{丨m丨+\frac{3}{丨m丨}}$≤$\frac{8\sqrt{3}}{2\sqrt{丨m丨×\frac{3}{丨m丨}}}$4,
当且仅当丨m丨=$\frac{3}{丨m丨}$时,即m=±$\sqrt{3}$,
∴四边形ABF1F2面积的最大值4.
点评 本题考查的标准方程及简单几何性质,直线与椭圆及圆的位置关系,考查韦达定理,弦长公式,三角形的面积公式,考查点到直线的距离公式,基本不等式的应用,属于难题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
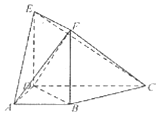 如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,
如图,梯形ABCD中,∠BAD=∠ADC=90°,CD=2AD=2,四边形BDEF为矩形,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x) | B. | -f(x) | C. | g(x) | D. | -g(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com