
分析 利用分母不为0,开偶次方,被开方数非负,列出不等式或表达式组求解即可.
解答 解:(1)要使函数有意义,可得x-2≠0,解得x≠2.函数的定义域为{x|x≠2,x∈R}.
(2)要使函数有意义,
可得3x+2≥0,解得x$≥-\frac{2}{3}$,
函数的定义域为:{x|x$≥-\frac{2}{3}$}.
(3)要使函数有意义,可得:-x2+2≥0,x∈Z,解得x=-1,0,1.
函数的定义域为:{-1,0,1}.
(4)要使f(x)=$\frac{(x+1)^{2}}{x+1}$-$\sqrt{1-x}$有意义.可得:$\left\{\begin{array}{l}{x+1≠0}\\{1-x≥0}\end{array}\right.$,
解得x<-1或-1<x≤1.
函数的定义域为:{x|x<-1或-1<x≤1}.
点评 本题考查函数的定义域的求法,考查计算能力.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
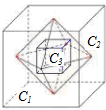 如图,记棱长为1的正方体C1,以C1各个面的中心为顶点的正八面体为C2,以C2各面的中心为顶点的正方体为C3,以C3各个面的中心为顶点的正八面体为C4,…,以此类推得一系列的多面体Cn,设Cn的棱长为an,则数列{an}的各项和为$\frac{6+3\sqrt{2}}{4}$.
如图,记棱长为1的正方体C1,以C1各个面的中心为顶点的正八面体为C2,以C2各面的中心为顶点的正方体为C3,以C3各个面的中心为顶点的正八面体为C4,…,以此类推得一系列的多面体Cn,设Cn的棱长为an,则数列{an}的各项和为$\frac{6+3\sqrt{2}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com