【题目】用五种不同颜色给三棱台
的六个顶点染色，要求每个点染一种颜色，且每条棱的两个端点染不同颜色.则不同的染色方法有___________种.
【答案】1920.
【解析】
分析：分两步来进行，先涂
，再涂
，然后分若5种颜色都用上、若5种颜色只用4种、若5种颜色只用3种这三种情况，分别求得结果，再相加，即可得结果.
详解：分两步来进行，先涂，再涂.
第一类：若5种颜色都用上，先涂，方法有
种，再涂中的两个点，方法有
种，最后剩余的一个点只有2种涂法，故此时方法共有
种；
第二类：若5种颜色只用4种，首先选出4种颜色，方法有
种；
先涂，方法有
种，再涂中的一个点，方法有3种，最后剩余的两个点只有3种涂法，故此时方法共有
种；
第三类：若5种颜色只用3种，首先选出3种颜色，方法有
种；
先涂，方法有
种，再涂，方法有2种，故此时方法共有
种；
综上可得，不同涂色方案共有
种，
故答案是1920.
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
的离心率为
，且椭圆
过点
.过点
做两条相互垂直的直线
、
分别与椭圆
交于
、
、
、
四点.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）若
， 
，探究：直线
是否过定点？若是，请求出定点坐标；若不是，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题：今有官司差夫一千八百六十四人筑堤，只云初日差六十四人，次日转多七人.”其大意为“官府陆续派遣1864人前往修筑堤坝，第一天派出64人，从第二天开始每天派出的人数比前一天多7人.”在该问题中的1864人全部派遣到位需要的天数为（ ）
A. 9B. 16C. 18D. 20
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知圆
，抛物线
的顶点为
，准线的方程为
，
为抛物线上的动点，过点
作圆
的两条切线与
轴交于
.
（Ⅰ）求抛物线的方程；
（Ⅱ）若
，求△
面积
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，△ABC为正三角形，EC⊥平面ABC，BD∥CE，且CE＝CA＝2BD，M是EA的中点．求证：
(1)DE＝DA；
(2)平面BDM⊥平面ECA；
(3)平面DEA⊥平面ECA.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一半径为2米的水轮如图所示，水轮圆心
距离水面1米;已知水轮按逆时针做匀速转动，每3秒转一圈，如果当水轮上点
从水中浮现时(图中点
)开始计算时间.
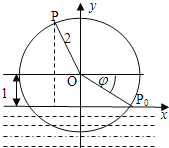
(1)试将点距离水面的高度
(单位:米)表示为时间
(单位:秒)的函数
;
(2)点第一次到达最高点大约要多长时间?
(3)求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某旅游区每年各个月份接待游客的人数近似地满足周期性规律，因而第
个月从事旅游服务工作的人数
可近似地用函数
来刻画，其中正整数表示月份且
，例如
表示1月份，
和
是正整数，
，
. 统计发现，该地区每年各个月份从事旅游服务工作的人数有以下规律：
① 每年相同的月份，该地区从事旅游服务工作的人数基本相同；
② 该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差400人；
③ 2月份该地区从事旅游服务工作的人数为100人，随后逐月递增直到8月份达到最多.
（1）试根据已知信息，求的表达式；
（2）一般地，当该地区从事旅游服务工作的人数在400或400以上时，该地区也进入了一年中的旅游“旺季”，那么，一年中的哪几个月是该地区的旅游“旺季”？请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
