
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
设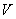 是已知平面
是已知平面 上所有向量的集合,对于映射
上所有向量的集合,对于映射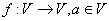 ,记
,记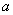 的象为
的象为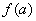 。若映射
。若映射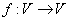 满足:对所有
满足:对所有
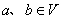 及任意实数
及任意实数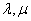 都有
都有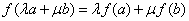 ,则
,则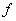 称为平面
称为平面 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设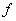 是平面
是平面 上的线性变换,
上的线性变换,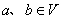 ,则
,则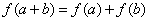
②若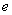 是平面
是平面 上的
上的 单位向量,对
单位向量,对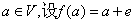 ,则
,则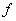 是平面
是平面 上的线性变换;
上的线性变换;
③对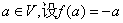 ,则
,则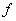 是平面
是平面 上的线性变换;
上的线性变换;
④设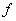 是平面
是平面 上的线性变换,
上的线性变换,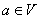 ,则对任意实数
,则对任意实数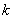 均有
均有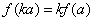 。
。
其中的真命题是  (写出所有真命题的编号)
(写出所有真命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是 。
。
(I)求函数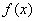 的解析式;
的解析式;
(II)设函数 ,若
,若 的极值存在,求实数
的极值存在,求实数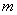 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设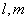 是两条不同的直线,
是两条不同的直线,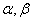 是两个不重合的平面,给出下列四个命题:
是两个不重合的平面,给出下列四个命题:
①若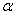 ∥
∥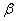 ,
,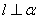 ,则
,则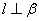 ; ②若
; ②若 ∥
∥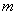 ,
,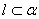 ,
,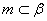 ,则
,则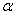 ∥
∥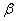 ;
;
③若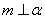 ,
,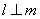 ,则
,则 ∥
∥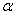 ; ④若
; ④若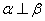 ,
,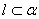 ,
,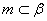 ,则
,则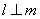 .
.
其中真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
如下图,在杨辉三角形中,从上往下数共有n(n∈N*)行,在这些数中非1的数字之和是
________________.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com