
| A. | [$\frac{5}{4}$,$\frac{5}{3}$] | B. | [$\frac{3}{2}$,++∞) | C. | (1,4] | D. | [$\frac{3}{2}$,4] |
分析 如图所示,设双曲线C2的离心率为e1,椭圆与双曲线的半焦距为c.由椭圆的定义及其题意可得:|MF2|=|F1F2|=2c,|MF1|=2a-2c.由双曲线的定义可得:2a-2c-2c=2a1,即a-2c=a1,可得$\frac{1}{e}$-2=$\frac{1}{{e}_{1}}$,利用e∈[$\frac{3}{8}$,$\frac{4}{9}$],即可得出双曲线C2的离心率的取值范围.
解答 解:如图所示,
设双曲线C2的离心率为e1.
椭圆与双曲线的半焦距为c.
由椭圆的定义及其题意可得:|MF2|=|F1F2|=2c,|MF1|=2a-2c.
由双曲线的定义可得:2a-2c-2c=2a1,即a-2c=a1,
∴$\frac{1}{e}$-2=$\frac{1}{{e}_{1}}$,
∵e∈[$\frac{3}{8}$,$\frac{4}{9}$],∴$\frac{1}{e}$∈[$\frac{9}{4}$,$\frac{8}{3}$],
∴$\frac{1}{{e}_{1}}$∈[$\frac{1}{4}$,$\frac{2}{3}$].
∴e1∈[$\frac{3}{2}$,4].
故选:D.
点评 本题考查了椭圆与双曲线的定义标准方程及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
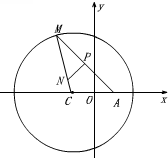 已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,线段MA的垂直平分线交MC于点N,设点N的轨迹为曲线E.
已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,线段MA的垂直平分线交MC于点N,设点N的轨迹为曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com