
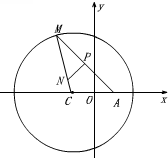
 已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,线段MA的垂直平分线交MC于点N,设点N的轨迹为曲线E.
已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,线段MA的垂直平分线交MC于点N,设点N的轨迹为曲线E.分析 (1)由题意可知:丨NC丨=r-丨NM丨,丨NC丨+丨NM丨=r=2$\sqrt{2}$>丨AC丨,点N的轨迹是以A、C 为焦点的椭圆,2a=2$\sqrt{2}$,即a=$\sqrt{2}$,c=1,椭圆的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)由(1)可知:设直线GH的方程为:y=kx+2,代入椭圆方程,由韦达定理可知:x1+x2=-$\frac{4k}{\frac{1}{2}+{k}^{2}}$,x1•x2=$\frac{3}{\frac{1}{2}+{k}^{2}}$,由$\overrightarrow{FG}=\frac{3}{5}\overrightarrow{FH}$,求得x1=$\frac{3}{5}$x2,代入即可求得k2=2>$\frac{3}{2}$,即可求得直线方程,当直线GH斜率不存在时,不符合题意.
解答 解:(1)设点N的坐标为(x,y),
NP是线段AM的垂直平分线,
又点N在CM上,圆C:(x+1)2+y2=8,半径是 r=2$\sqrt{2}$,
∴丨NC丨=r-丨NM丨,
∴丨NC丨+丨NM丨=r=2$\sqrt{2}$>丨AC丨,
∴点N的轨迹是以A、C 为焦点的椭圆,
设椭圆的方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
∴2a=2$\sqrt{2}$,即a=$\sqrt{2}$,c=1,
由b2=a2-c2=1,
∴椭圆的方程为:$\frac{{x}^{2}}{2}+{y}^{2}=1$,
∴曲线E方程:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(2)设G(x1,y1),H(x2,y2),
当直线GH斜率存在时,设直线GH的斜率为k
则直线GH的方程为:y=kx+2,
∴$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:($\frac{1}{2}$+k2)x2+4kx+3=0,
由△>0,解得:k2>$\frac{3}{2}$,
x1+x2=-$\frac{4k}{\frac{1}{2}+{k}^{2}}$,x1•x2=$\frac{3}{\frac{1}{2}+{k}^{2}}$,
又∵$\overrightarrow{FG}$=(x1,y1-2),$\overrightarrow{FH}$=(x2,y2-2),
∵$\overrightarrow{FG}=\frac{3}{5}\overrightarrow{FH}$,
∴x1=$\frac{3}{5}$x2,
整理得:$\frac{3}{5}$•(-$\frac{5k}{1+2{k}^{2}}$)2=$\frac{6}{1+2{k}^{2}}$,即k2=2>$\frac{3}{2}$,
解得:k=±$\sqrt{2}$,
∴直线l的方程为:y=±$\sqrt{2}$x+2,
当直线GH斜率不存在时,直线的l方程为x=0,
$\overrightarrow{FG}$=$\frac{1}{3}$$\overrightarrow{FH}$与$\overrightarrow{FG}=\frac{3}{5}\overrightarrow{FH}$矛盾,
故直线GH斜率不存在时,直线方程不成立,
∴直线l的方程为:y=±$\sqrt{2}$x+2.
点评 本题考查椭圆的标准方程及椭圆的定义,考查直线与椭圆的位置关系,考查韦达定理,向量的坐标运算,考查分类讨论思想,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{|x|}{x}$ | B. | y=${a^{{{log}_a}x}}$(a>0且a≠1) | ||
| C. | y=$\sqrt{x^2}$ | D. | y=logaax(a>0且a≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{5}{4}$,$\frac{5}{3}$] | B. | [$\frac{3}{2}$,++∞) | C. | (1,4] | D. | [$\frac{3}{2}$,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com