
| A. | y=$\frac{|x|}{x}$ | B. | y=${a^{{{log}_a}x}}$(a>0且a≠1) | ||
| C. | y=$\sqrt{x^2}$ | D. | y=logaax(a>0且a≠1) |
分析 分别判断两个函数的定义域和对应法则是否相同即可.
解答 解:A.y=$\frac{|x|}{x}$=$\left\{\begin{array}{l}{1,}&{x>0}\\{-1,}&{x<0}\end{array}\right.$,与y=x的定义域不同,对应法则不同,不是同一函数,
B.y=${a^{{{log}_a}x}}$=x,(x>0)(a>0且a≠1)=1,(x≠0),两个函数的定义域不相同,不是同一函数,
Cy=$\sqrt{x^2}$=|x|,两个函数的定义域相同,但对应法则不相同,不是椭圆函数,
D.y=logaax=x,两个函数的定义域相同,对应法则相同,是相等函数,
故选:D
点评 本题主要考查同一函数的判断,根据定义判断两个函数的定义域和对应法则是否相同是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 评估的平均得分 | (0,6) | [6,8) | [8,10] |
| 全市的总体交通状况等级 | 不合格 | 合格 | 优秀 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 5 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
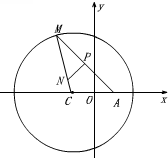 已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,线段MA的垂直平分线交MC于点N,设点N的轨迹为曲线E.
已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,线段MA的垂直平分线交MC于点N,设点N的轨迹为曲线E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,5} | B. | {0,1,2,3,4,5} | C. | {0,1,2} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图示:半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一
如图示:半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com