练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．运行如图所示框图的相应程序，若输入a，b的值分别为0.25和4，则输出M的值是（　　）
    A．0B．1C．2D．-1

    分析 分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算分段函数M=$\left\{\begin{array}{l}{a×b-1，a≤b}\\{a×b+1，a＞b}\end{array}\right.$的值．

    解答 解：分析程序中各变量、各语句的作用，
    再根据流程图所示的顺序，可知：
    该程序的作用是计算分段函数M=$\left\{\begin{array}{l}{a×b-1，a≤b}\\{a×b+1，a＞b}\end{array}\right.$的值．
    ∵a=0.25，b=4，
    ∴a＜b
    ∴M=0.25×4-1=0
    故选A．

    点评 本题考查的知识眯是程序框图，其中根据程序框图分析出程序框图的功能是解答本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．2和8的等比中项有4和-4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知向量$\overrightarrow{BA}$=（-$\frac{1}{2}，\frac{\sqrt{3}}{2}$），$\overrightarrow{BC}$=（$\frac{1}{2}，\frac{\sqrt{3}}{2}$），则∠ABC=（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在直角坐标系xOy中，以M（-1，0）为圆心的圆与直线$x-\sqrt{3}y-3=0$相切．
    （1）求圆M的方程；
    （2）过点（0，3）的直线l被圆M截得的弦长为$2\sqrt{3}$，求直线l的方程．
    （3）已知A（-2，0），B（2，0），圆M内的动点P满足|PA|•|PB|=|PO|2，求$\overrightarrow{PA}•\overrightarrow{PB}$的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．设F1，F2分别为椭圆$\frac{x^2}{25}+\frac{y^2}{16}=1$的左右焦点，P为椭圆上一点，若△F1F2P为直角三角形，该三角形的面积为$\frac{48}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．为了解宝鸡市的交通状况，现对其6条道路进行评估，得分分别为：5，6，7，8，9，10．规定评估的平均得分与全市的总体交通状况等级如表：
    评估的平均得分（0，6）[6，8）[8，10]
    全市的总体交通状况等级不合格合格优秀
    （1）求本次评估的平均得分，并参照上表估计该市的总体交通状况等级；
    （2）用简单随机抽样方法从这6条道路中抽取2条，它们的得分组成一个样本，求该样本的平均数与总体的平均数之差的绝对值不超过0.5的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若函数y=${（\frac{1}{2}）^{|x|}}$+m有零点，则实数m的取值范围是[-1，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

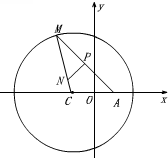    2．已知圆C：（x+1）2+y2=8，定点A（1，0），M为圆上一动点，线段MA的垂直平分线交MC于点N，设点N的轨迹为曲线E．
    （1）求曲线E方程；
    （2）若经过F（0，2）的直线l交曲线E于不同的两点G，H（点G在点F，H之间），且满足$\overrightarrow{FG}=\frac{3}{5}\overrightarrow{FH}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．比较${2^{0.2}}，{2^{0.5}}，lo{g_3}\frac{3}{2}$的大小20.5＞20.2＞$lo{g}_{3}\frac{3}{2}$．

    查看答案和解析>>

    同步练习册答案